题目内容
【题目】已知定义域为R的奇函数![]() ,满足
,满足 ,则下列叙述正确的为( )
,则下列叙述正确的为( )
①存在实数k,使关于x的方程![]() 有7个不相等的实数根
有7个不相等的实数根
②当![]() 时,恒有
时,恒有![]()
③若当![]() 时,
时,![]() 的最小值为1,则
的最小值为1,则![]()
④若关于![]() 的方程
的方程![]() 和
和![]() 的所有实数根之和为零,则
的所有实数根之和为零,则![]()
A.①②③B.①③C.②④D.①②③④
【答案】B
【解析】
对于①,当![]() 时,直线
时,直线![]() 与函数在第一象限有3个零点,关于x的方程
与函数在第一象限有3个零点,关于x的方程![]() 有7个不相等的实数根,所以①正确;
有7个不相等的实数根,所以①正确;
对于②,当![]() 时,函数
时,函数![]() 不是单调函数,所以②不正确;
不是单调函数,所以②不正确;
对于③,令![]() 所以
所以![]() ,则
,则![]() ,所以③正确;
,所以③正确;
对于④,通过数形结合分析得到其是错误的.
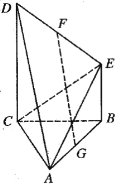
对于①,函数的图象如图所示,由于函数是奇函数,所以只要考查![]() 的零点个数,
的零点个数,
由于![]() ,所以只要考虑
,所以只要考虑![]() 的零点有3个即可.
的零点有3个即可.
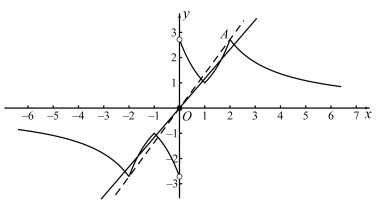
由题得![]() ,所以直线
,所以直线![]() 的斜率为
的斜率为![]() ,此时直线
,此时直线![]() 与函数的图象有5个交点,当
与函数的图象有5个交点,当![]() 时,直线
时,直线![]() 与函数在第一象限有3个零点,关于x的方程
与函数在第一象限有3个零点,关于x的方程![]() 有7个不相等的实数根,所以①正确;
有7个不相等的实数根,所以①正确;
对于②,当![]() 时,函数
时,函数![]() 不是单调函数,所以
不是单调函数,所以![]() 不成立,所以②不正确;
不成立,所以②不正确;
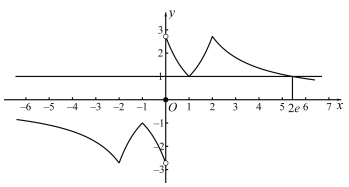
对于③,令![]() 所以
所以![]() ,当
,当![]() 时,
时,![]() 的最小值为1,则
的最小值为1,则![]() ,所以③正确;
,所以③正确;
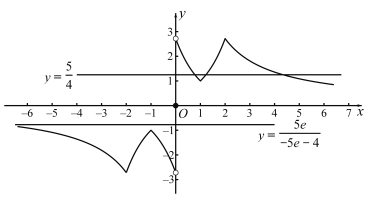
对于④,由于函数![]() 是奇函数,关于
是奇函数,关于![]() 的方程
的方程![]() 和
和![]() 的所有实数根之和为零,
的所有实数根之和为零,
当![]() 时,
时,![]() 有三个实根,
有三个实根,![]() ,
,
则![]() ,
,
所以![]() 的所有实数根之和为
的所有实数根之和为![]() .
.
令 所以
所以![]() 错误.
错误.
故选:B.

 阅读快车系列答案
阅读快车系列答案【题目】某公司为了对某种商品进行合理定价,需了解该商品的月销售量![]() (单位:万件)与月销售单价
(单位:万件)与月销售单价![]() (单位:元/件)之间的关系,对近
(单位:元/件)之间的关系,对近![]() 个月的月销售量
个月的月销售量![]() 和月销售单价
和月销售单价![]()
![]() 数据进行了统计分析,得到一组检测数据如表所示:
数据进行了统计分析,得到一组检测数据如表所示:
月销售单价 |
|
|
|
|
|
|
月销售量 |
|
|
|
|
|
|
(1)若用线性回归模型拟合![]() 与
与![]() 之间的关系,现有甲、乙、丙三位实习员工求得回归直线方程分别为:
之间的关系,现有甲、乙、丙三位实习员工求得回归直线方程分别为:![]() ,
,![]() 和
和![]() ,其中有且仅有一位实习员工的计算结果是正确的.请结合统计学的相关知识,判断哪位实习员工的计算结果是正确的,并说明理由;
,其中有且仅有一位实习员工的计算结果是正确的.请结合统计学的相关知识,判断哪位实习员工的计算结果是正确的,并说明理由;
(2)若用![]() 模型拟合
模型拟合![]() 与
与![]() 之间的关系,可得回归方程为
之间的关系,可得回归方程为![]() ,经计算该模型和(1)中正确的线性回归模型的相关指数
,经计算该模型和(1)中正确的线性回归模型的相关指数![]() 分别为
分别为![]() 和
和![]() ,请用
,请用![]() 说明哪个回归模型的拟合效果更好;
说明哪个回归模型的拟合效果更好;
(3)已知该商品的月销售额为![]() (单位:万元),利用(2)中的结果回答问题:当月销售单价为何值时,商品的月销售额预报值最大?(精确到
(单位:万元),利用(2)中的结果回答问题:当月销售单价为何值时,商品的月销售额预报值最大?(精确到![]() )
)
参考数据:![]() .
.
【题目】为考察某动物疫苗预防某种疾病的效果,现对200只动物进行调研,并得到如下数据:
未发病 | 发病 | 合计 | |
未注射疫苗 | 20 | 60 | 80 |
注射疫苗 | 80 | 40 | 120 |
合计 | 100 | 100 | 200 |
(附: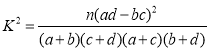 )
)
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
则下列说法正确的:( )
A.至少有99.9%的把握认为“发病与没接种疫苗有关”
B.至多有99%的把握认为“发病与没接种疫苗有关”
C.至多有99.9%的把握认为“发病与没接种疫苗有关”
D.“发病与没接种疫苗有关”的错误率至少有0.01%