题目内容
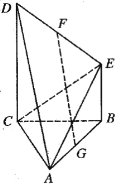
【题目】如图,已知四锥![]() 中,
中,![]() ,底面ABCD为形,
,底面ABCD为形,![]() ,点E为的AD中点.
,点E为的AD中点.
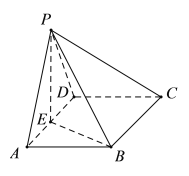
(1)证明:平面![]() 平面PBE;
平面PBE;
(2)若![]() ,二面角
,二面角![]() 的余弦值为
的余弦值为![]() ,且
,且![]() ,求PE的长.
,求PE的长.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)证明![]() ,
,![]() ,又
,又![]() ,可证得
,可证得![]() ,
,![]() ,则可证得
,则可证得![]() 平面PBE,从而可证得平面
平面PBE,从而可证得平面![]() 平面PBE;
平面PBE;
(2)设![]() ,易证
,易证![]() 两两垂直,可建立空间直角坐标系,用坐标法表示出,二面角
两两垂直,可建立空间直角坐标系,用坐标法表示出,二面角![]() 的余弦值为
的余弦值为![]() ,从而求得
,从而求得![]() .
.
(1)证明:连结BD,∵四边形ABCD是菱形,又![]() ,
,
∴![]() 是等边三角形,又E为AD中点,
是等边三角形,又E为AD中点,
∴![]() ,
,![]() ,
,
又![]() ,∴
,∴![]() ,
,![]() ,
,
又BE,![]() 平面PBE,
平面PBE,![]() ,
,
∴![]() 平面PBE,又
平面PBE,又![]() 平面PBC,∴平面
平面PBC,∴平面![]() 平面PBE.
平面PBE.
(2)由(1)得![]() ,又
,又![]() ,∴易知
,∴易知![]() 平面ABCD,
平面ABCD,
∴![]() ,由(1)得
,由(1)得![]() ,
,![]() .
.
以E为原点,![]() ,
,![]() ,
,![]() 分别为x,y,z轴建立空间直角坐标系,如图所示:
分别为x,y,z轴建立空间直角坐标系,如图所示:
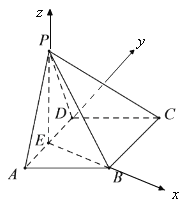
设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
设![]() 为平面PAD的法向量,
为平面PAD的法向量,
则 ,即
,即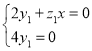 ,∴取
,∴取![]() ,则
,则![]() ,
,
设![]() 为平面PAB的法向量,
为平面PAB的法向量,
则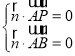 ,
,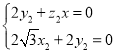 ,∴取
,∴取![]() ,则
,则![]() ,
,
则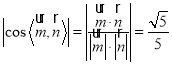 ,∴
,∴![]() ,∴
,∴![]() .
.

练习册系列答案
相关题目
【题目】某公司为了对某种商品进行合理定价,需了解该商品的月销售量![]() (单位:万件)与月销售单价
(单位:万件)与月销售单价![]() (单位:元/件)之间的关系,对近
(单位:元/件)之间的关系,对近![]() 个月的月销售量
个月的月销售量![]() 和月销售单价
和月销售单价![]()
![]() 数据进行了统计分析,得到一组检测数据如表所示:
数据进行了统计分析,得到一组检测数据如表所示:
月销售单价 |
|
|
|
|
|
|
月销售量 |
|
|
|
|
|
|
(1)若用线性回归模型拟合![]() 与
与![]() 之间的关系,现有甲、乙、丙三位实习员工求得回归直线方程分别为:
之间的关系,现有甲、乙、丙三位实习员工求得回归直线方程分别为:![]() ,
,![]() 和
和![]() ,其中有且仅有一位实习员工的计算结果是正确的.请结合统计学的相关知识,判断哪位实习员工的计算结果是正确的,并说明理由;
,其中有且仅有一位实习员工的计算结果是正确的.请结合统计学的相关知识,判断哪位实习员工的计算结果是正确的,并说明理由;
(2)若用![]() 模型拟合
模型拟合![]() 与
与![]() 之间的关系,可得回归方程为
之间的关系,可得回归方程为![]() ,经计算该模型和(1)中正确的线性回归模型的相关指数
,经计算该模型和(1)中正确的线性回归模型的相关指数![]() 分别为
分别为![]() 和
和![]() ,请用
,请用![]() 说明哪个回归模型的拟合效果更好;
说明哪个回归模型的拟合效果更好;
(3)已知该商品的月销售额为![]() (单位:万元),利用(2)中的结果回答问题:当月销售单价为何值时,商品的月销售额预报值最大?(精确到
(单位:万元),利用(2)中的结果回答问题:当月销售单价为何值时,商品的月销售额预报值最大?(精确到![]() )
)
参考数据:![]() .
.