题目内容
(本小题满分14分)
已知函数f(x)的定义域为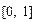 ,
, 且同时满足:①f(1)=3;②
且同时满足:①f(1)=3;②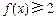 对一切
对一切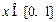 恒成立;③若
恒成立;③若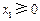 ,
,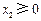 ,
,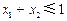 ,则
,则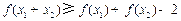 .
.
①求函数f(x)的最大值 和最小值;
和最小值;
②试比较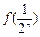 与
与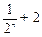
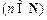 的大小;
的大小;
③某同学发现:当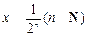 时,有
时,有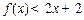 ,由此他提出猜想:对一切
,由此他提出猜想:对一切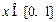 ,都有
,都有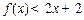 ,请你判断此猜想是否正确,并说明理由.
,请你判断此猜想是否正确,并说明理由.
已知函数f(x)的定义域为
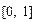 ,
, 且同时满足:①f(1)=3;②
且同时满足:①f(1)=3;②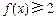 对一切
对一切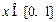 恒成立;③若
恒成立;③若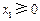 ,
,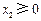 ,
,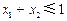 ,则
,则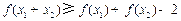 .
.①求函数f(x)的最大值
 和最小值;
和最小值;②试比较
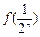 与
与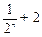
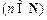 的大小;
的大小;③某同学发现:当
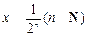 时,有
时,有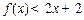 ,由此他提出猜想:对一切
,由此他提出猜想:对一切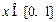 ,都有
,都有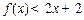 ,请你判断此猜想是否正确,并说明理由.
,请你判断此猜想是否正确,并说明理由.(1)当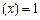 时,
时, 取得最大值
取得最大值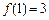 ,当
,当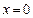 时,
时, 取得最小值
取得最小值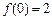
(2)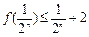 (3)对任意
(3)对任意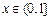 ,
,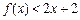 恒成立
恒成立
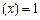 时,
时, 取得最大值
取得最大值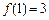 ,当
,当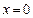 时,
时, 取得最小值
取得最小值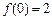
(2)
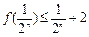 (3)对任意
(3)对任意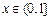 ,
,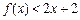 恒成立
恒成立解:(1)设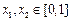 ,
,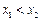 ,则
,则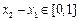
∴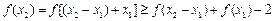
∴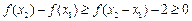
∵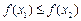 ,则当
,则当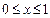 时,
时,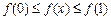
∴当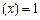 时,
时, 取得最大值
取得最大值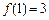 ;
;
又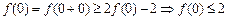 而
而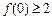 ∴
∴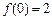
当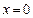 时,
时, 取得最小值
取得最小值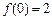
(2)在③中令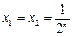 ,得
,得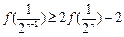
∴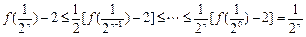
∴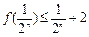
(3)对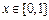 ,总存在
,总存在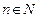 ,满足
,满足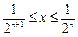
由(1)(2)得: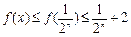
又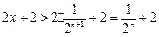 ∴
∴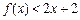
综上所述,对任意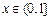 ,
,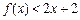 恒成立
恒成立
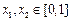 ,
,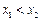 ,则
,则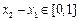
∴
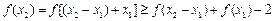
∴
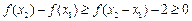
∵
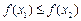 ,则当
,则当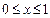 时,
时,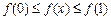
∴当
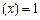 时,
时, 取得最大值
取得最大值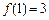 ;
;又
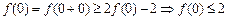 而
而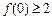 ∴
∴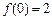
当
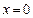 时,
时, 取得最小值
取得最小值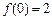
(2)在③中令
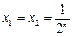 ,得
,得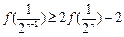
∴
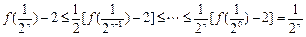
∴
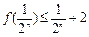
(3)对
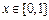 ,总存在
,总存在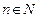 ,满足
,满足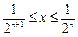
由(1)(2)得:
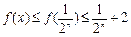
又
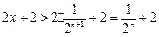 ∴
∴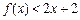
综上所述,对任意
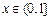 ,
,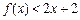 恒成立
恒成立
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
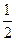 )="0," 则满足
)="0," 则满足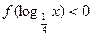 的集合为 ( )
的集合为 ( ) 10分)定义在R上的函数
10分)定义在R上的函数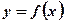 ,对任意的
,对任意的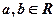 ,满足
,满足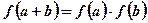 ,当
,当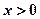 时,有
时,有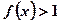 ,其中
,其中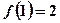 .
.
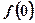 的值;
的值;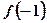 的值并判断该函数的奇偶性;
的值并判断该函数的奇偶性;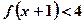 的解集.
的解集.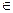 R,记
R,记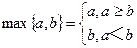 ,函数f(x)=
,函数f(x)=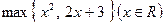 的单调递减区间为__ __
的单调递减区间为__ __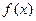 满足:对任意的
满足:对任意的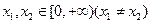 ,有
,有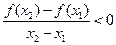 . 则 ( )
. 则 ( )



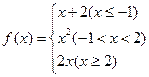 ,若
,若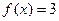 ,则
,则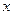 的值是( )
的值是( )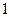
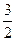
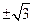
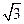
 若
若 ,则
,则 的取值范围 ( )
的取值范围 ( )



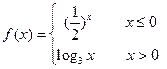 ,则
,则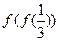 = .
= .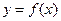 又是减函数,且
又是减函数,且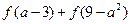 <0,则a的取值范围是( )
<0,则a的取值范围是( )


