题目内容
【题目】在底面半径为6的圆柱内,有两个半径也为6的球面,两球的球心距为13,若作一个平面与两个球都相切,且与圆柱面相交成一椭圆,则椭圆的长轴长为 .
【答案】13
【解析】试题设两个球的球心分别为O1、O2,椭圆的长轴为AB,作出由AB与O1O2确定平面α与两个球及圆柱的截面,并过A作O1O2的垂线,交圆柱的母线于点C,连接O1与AB切球O1的切点D.分别在Rt△O1DE中和Rt△ABC中,利用∠BAC=∠DO1E和余弦的定义,结合题中的数据建立关系式,即可解出AB的长,即得该椭圆的长轴长.
解:设两个球的球心分别为O1、O2,所得椭圆的长轴为AB,
直线AB与O1O2交于点E,设它们确定平面α,
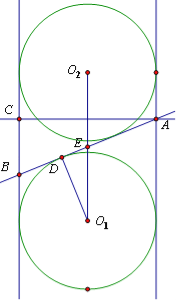
作出平面α与两个球及圆柱的截面,如图所示
过A作O1O2的垂线,交圆柱的母线于点C,设AB切球O1的大圆于点D,连接O1D
∵Rt△O1DE中,O1E=![]() O1O2=
O1O2=![]() ,O1D=6
,O1D=6
∴cos∠DO1E=![]() =
=![]()
∵锐角∠DO1E与∠BAC的两边对应互相垂直
∴∠BAC=∠DO1E,
得Rt△ABC中,cos∠BAC=![]() =
=![]()
∵AC长等于球O1的直径,得AC=12
∴椭圆的长轴AB=13
故答案为:13

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目