Question

【题目】正四棱锥的底面正方形边长是3，是在底面上的射影，，是上的一点，过且与、都平行的截面为五边形．

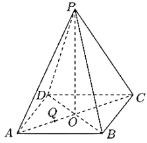
（1）在图中作出截面，并写出作图过程；

（2）求该截面面积的最大值．

Answer 1

【答案】（1）见解析；（2）9.

【解析】

（1）根据题意，作辅助线，过作， 且过点作，交于点，过点作交于点，连接， 即可得出截面；

（2）由题意可知，截面，截面，根据平面，利用线面垂直的性质和判定，可证出平面，则，进而得出，所以截面是由两个全等的直角梯形组成，设，则，截面面积为，根据，代入计算，最后利用二次函数求得最大值.

解：（1）由题可知，是上的一点，过且与、都平行的截面为五边形，

过作，交于点，交于点，

过作，交于点，

再过点作，交于点，

过点作交于点，连接，

，，，

，

所以共面，平面，

，平面，

平面，同理平面.

所以过且与、都平行的截面如下图：

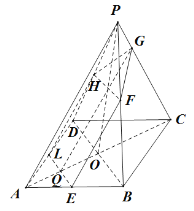
（2）由题意可知，截面，截面，

，，

而是在底面上的射影，，

平面，，

，且，

所以平面，则，

，

又， 为正四棱锥，

，故，

于是，

因此截面是由两个全等的直角梯形组成，

因，则为等腰直角三角形，

设，则，

所以，，

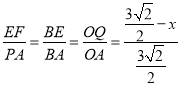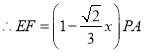，同理得，，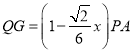

又因为，

设截面面积为，

所以，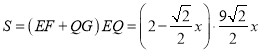

即：，

当且仅当时，有最大值为9.

所以截面的面积最大值为9.