题目内容
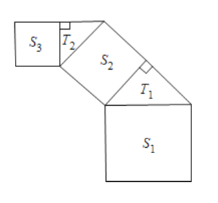
【题目】如图所示，正方形上连接等腰直角三角形，直角三角形上再连接正方形……如此无限重复下去，设正方形面积为
，三角形面积为
.当第一个正方形的边长为2时，则这些正方形和三角形的面积的总和为______.
【答案】10
【解析】
先由题意，求出
，
，得到正方形的面积
构成以
为首项，以
为公比的等比数列，三角形的面积
构成以
为首项，以为公比的等比数列，根据等比数列的前
项和公式，以及极限的运算法则，即可得出结果.
因为第一个正方形的边长为2，所以
；
因此第一个三角形的直角边长为
，其面积为：
；
由题意，正方形的面积构成以为首项，以为公比的等比数列；
所以其前项和为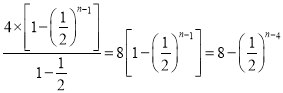
；
三角形的面积构成以为首项，以为公比的等比数列；
所以其前项和为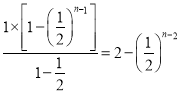
，
因此这些正方形和三角形的面积的总和为:
.
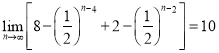故答案为：
.
练习册系列答案
相关题目
