题目内容
14.在数列{an}中,a1=1,an+1=(-1)n(an +1),记Sn为{an}的前n项和,则S2015=( )| A. | -1008 | B. | -1007 | C. | -1006 | D. | -1005 |
分析 an+1=(-1)n(an +1),可得a2k+1=a2k+1,a2k=-(a2k-1+1),于是a2k+1=-a2k-1,a2k+a2k-2=-2.即可得出.
解答 解:∵an+1=(-1)n(an +1),
∴a2k+1=a2k+1,a2k=-(a2k-1+1),
∴a2k+1=-a2k-1,a2k+a2k-2=-2.
∴S2015=(a1+a3+…+a2015)+(a2+a4+…+a2014)
=a1+(-2)×503+a2
=1-1006-2
=-1007.
故选:B.
点评 本题考查了数列“分组求和”方法、递推关系的应用、分类讨论方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.函数f(x)=x1nx的零点为( )
| A. | 0或1 | B. | 1 | C. | (1,0) | D. | (0,0)或(1,0) |
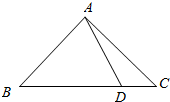 如图,在△ABC中,已知B=$\frac{π}{4}$,D是BC边上一点,AD=10,AC=14,DC=6,则AB=5$\sqrt{6}$.
如图,在△ABC中,已知B=$\frac{π}{4}$,D是BC边上一点,AD=10,AC=14,DC=6,则AB=5$\sqrt{6}$.