题目内容
已知过点P(-2,-2)作圆x2+y2+Dx-2y-5=0的两切线关于直线x-y=0对称,
设切点分别有A、B,求直线AB的方程.
解:由题可知,圆的圆心在直线x-y=0上, 或在过P(-2,-2)且与直线x-y=0垂直
或在过P(-2,-2)且与直线x-y=0垂直 的直线上,圆的圆心坐标
的直线上,圆的圆心坐标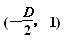
(1)当圆心在直线x-y=0上
有:-=1,解得D=-2
此时圆的 方程为:x2+y2-2x-2y-5=0
方程为:x2+y2-2x-2y-5=0
以(1,1),(-2,-2)为直径的圆的方程为:(x-1)(x+2)+(y-1)(y +2)=0
+2)=0
即x2+y2+x+y-4=0
故lAB的直线方程为:3x+3y+1=0
(2)当过P(-2,-2)且与直线x-y=0垂直的直线上
过P(-2,-2)且与直线x-y=0垂直的直线方程为:x+y+4=0
得D=10,故圆心坐标为(-5,1)
圆的方程为:x2+y2+10x-2y-5=0,得点P在圆内,故无切线方程。
解析

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设双曲线 的一条渐近线与抛物线y=x2+1只有一个公共点,则双曲线的离心率为( )
的一条渐近线与抛物线y=x2+1只有一个公共点,则双曲线的离心率为( )
A. | B.5 | C. | D. |
点 到图形
到图形 上每一个点的距离的最小值称为点
上每一个点的距离的最小值称为点 到图形
到图形 的距离,那么平面内到定圆
的距离,那么平面内到定圆 的距离与到定点
的距离与到定点 的距离相等的点的轨迹不可能是( )
的距离相等的点的轨迹不可能是( )
| A.圆 | B.椭圆 | C.双曲线的一支 | D.直线 |
双曲线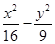 =1的焦点到渐近线的距离为( )
=1的焦点到渐近线的距离为( )
| A.2 | B.3 | C.4 | D.5 |
 N(1,0)的距离的比为。
N(1,0)的距离的比为。 ,1)直线
,1)直线 :
: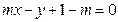
 ,直线
,直线 点;
点; 时,求m的值。
时,求m的值。 与圆O相切于C,交AB于E,且与AF垂直,垂足为G,连接AC.
与圆O相切于C,交AB于E,且与AF垂直,垂足为G,连接AC.
 ;
; .
. 相外切,并且与直线
相外切,并且与直线 相切于点
相切于点 ,求圆C的
,求圆C的 的方程为
的方程为 ,圆
,圆 的极坐标方程为
的极坐标方程为  .
.