题目内容
数列{an}中，a1=2，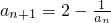
，（1）写出a2，a3，a4：（2）猜测{an}表达式，并用数学归纳法证明．
解：分别令n=1，2，3，代入递推公式得：
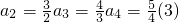（3分）
猜：
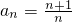（5分）
证明：n=1命题成立 （6分）
假设n=k成立，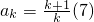
（7分）
当
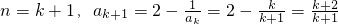（9分）
所以n∈N，命题成立． （10分）
分析：（1）由题意可得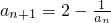，又a1=2，可求得a2，再由a2的值求 a3，再由a3 的值求出a4的值．
（2）猜想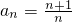，检验n=1时等式成立，假设n=k时命题成立，证明当n=k+1时命题也成立．
点评：本题考查数列的递推公式，用数学归纳法证明等式成立．证明当n=k+1时命题也成立，是解题的难点．
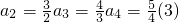（3分） 猜：
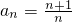（5分）证明：n=1命题成立 （6分）
假设n=k成立，
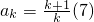（7分）当
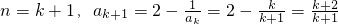（9分）所以n∈N，命题成立． （10分）
分析：（1）由题意可得
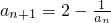，又a1=2，可求得a2，再由a2的值求 a3，再由a3 的值求出a4的值．（2）猜想
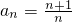，检验n=1时等式成立，假设n=k时命题成立，证明当n=k+1时命题也成立．点评：本题考查数列的递推公式，用数学归纳法证明等式成立．证明当n=k+1时命题也成立，是解题的难点．
练习册系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
数列{an}中，a1=
，an+an+1=
，n∈N*，则
（a1+a2+…+an）等于（ ）
| 1 |
| 5 |
| 6 |
| 5n+1 |
| lim |
| n→∞ |
A、
| ||
B、
| ||
C、
| ||
D、
|