题目内容
 如图,三棱锥P-ABC的底面ABC是以AC为斜边的直角三角形,且顶点P在底面的射影是△ABC外心,设PB=AB=1,BC=
如图,三棱锥P-ABC的底面ABC是以AC为斜边的直角三角形,且顶点P在底面的射影是△ABC外心,设PB=AB=1,BC=| 2 |
(1)求证:面PAC⊥面ABC;
(2)求侧棱PB与底面ABC所成的角;
(3)求侧面PAB与底面ABC所成二面角的正切值.
分析:(1)过P作PD⊥平面ABC,交点为D,易得D为斜边AC的中点,进而由面面垂直的判定定理,可得面PAC⊥面ABC;
(2)连结DB,由(1)中结论,结合线面夹角的定义,可得∠PBD是PB与面ABC所成的角,解△PBD可得侧棱PB与底面ABC所成的角;
(3)过D点作OD⊥AB,垂足为O,连PO,由三垂线定理可知PO⊥AB,即∠POD是侧面PAB与面ABC所成二面角的平面角,解△POD可得侧面PAB与底面ABC所成二面角的正切值.
(2)连结DB,由(1)中结论,结合线面夹角的定义,可得∠PBD是PB与面ABC所成的角,解△PBD可得侧棱PB与底面ABC所成的角;
(3)过D点作OD⊥AB,垂足为O,连PO,由三垂线定理可知PO⊥AB,即∠POD是侧面PAB与面ABC所成二面角的平面角,解△POD可得侧面PAB与底面ABC所成二面角的正切值.
解答: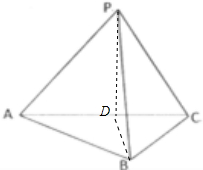 证明:(1)过P作PD⊥平面ABC,交点为D,
证明:(1)过P作PD⊥平面ABC,交点为D,
则D为△ABC外心,
故D为斜边AC的中点.
∵PD?面PAC
∴面PAC⊥面ABC.
解:(2)连DB,∵PD⊥面ABC.
∴∠PBD是PB与面ABC所成的角.
∵AB=1,BC=
,
故AC=
,
又BO=OC=
AC=
,PB=1,
在△POB中,cos∠PBO=
,
则∠PBO=
,
即侧棱PB与底面ABC所成角为
.
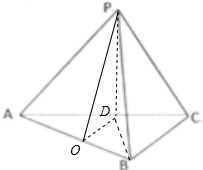
(3)过D点作OD⊥AB,垂足为O,连PO,由三垂线定理可知PO⊥AB,
∴∠POD是侧面PAB与面ABC所成二面角的平面角,
∵OD=
,PD=PBsin30°=
,
∴tan∠POD=
=
 证明:(1)过P作PD⊥平面ABC,交点为D,
证明:(1)过P作PD⊥平面ABC,交点为D,则D为△ABC外心,
故D为斜边AC的中点.
∵PD?面PAC
∴面PAC⊥面ABC.
解:(2)连DB,∵PD⊥面ABC.
∴∠PBD是PB与面ABC所成的角.
∵AB=1,BC=
| 2 |
故AC=
| 3 |

又BO=OC=
| 1 |
| 2 |
| ||
| 2 |
在△POB中,cos∠PBO=
| ||
| 2 |
则∠PBO=
| π |
| 6 |
即侧棱PB与底面ABC所成角为
| π |
| 6 |
(3)过D点作OD⊥AB,垂足为O,连PO,由三垂线定理可知PO⊥AB,
∴∠POD是侧面PAB与面ABC所成二面角的平面角,
∵OD=
| ||
| 2 |
| 1 |
| 2 |
∴tan∠POD=
| PD |
| DO |
| ||
| 2 |
点评:本题考查的知识点是平面与平面垂直的判定,直线与平面所成的角,二面角的平面角及求法,解答(1)的关键是判断出D为斜边AC的中点,解答(2)(3)的关键是构造出线面夹角及二面角的平面角.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
 如图,三棱锥P-ABC中,PC⊥平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD⊥平面PAB
如图,三棱锥P-ABC中,PC⊥平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD⊥平面PAB (2006•石景山区一模)如图,三棱锥P-ABC中,
(2006•石景山区一模)如图,三棱锥P-ABC中, (2012•湖南模拟)如图,三棱锥P-ABC中,侧面PAC⊥底面ABC,∠APC=90°,且AB=4,AP=PC=2,BC=2
(2012•湖南模拟)如图,三棱锥P-ABC中,侧面PAC⊥底面ABC,∠APC=90°,且AB=4,AP=PC=2,BC=2 (2012•德阳二模)如图,三棱锥P-ABC中,PA丄面ABC,∠ABC=90°,PA=AB=1,BC=2,则P-ABC的外接球的表面积为
(2012•德阳二模)如图,三棱锥P-ABC中,PA丄面ABC,∠ABC=90°,PA=AB=1,BC=2,则P-ABC的外接球的表面积为 如图在三棱锥P-ABC中,AB⊥PC,AC=2,BC=4,
如图在三棱锥P-ABC中,AB⊥PC,AC=2,BC=4,