题目内容
定义在R上的函数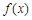 ,若对任意
,若对任意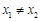 ,都有
,都有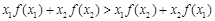 ,则称f(x)为“H函数”,给出下列函数:①
,则称f(x)为“H函数”,给出下列函数:①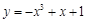 ;②
;② ;③
;③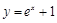 ;④
;④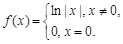 其中是“H函数”的个数为
其中是“H函数”的个数为
| A.1 | B.2 | C.3 | D.4 |
B
解析试题分析: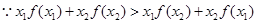 ,
,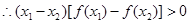 ;
;
即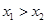 ,都有
,都有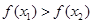 ,所以“H函数’是增函数;①
,所以“H函数’是增函数;①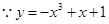 ,
,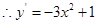 ,
,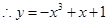 存在递减区间;②
存在递减区间;②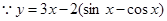 ,
,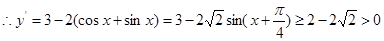 ,
,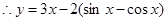 在R上递增;③
在R上递增;③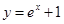 在R上递增,显然成立;④
在R上递增,显然成立;④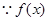 为偶函数,
为偶函数,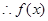 存在递减区间;故选B.
存在递减区间;故选B.
考点:新定义题、利用导数研究函数的单调性.

练习册系列答案
相关题目
若f(x)=x2-2x-4ln x,则f′(x)>0的解集为( )
| A.(0,+∞) | B.(-1,0)∪(2,+∞) |
| C.(2,+∞) | D.(-1,0) |
若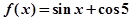 ,则该函数在点
,则该函数在点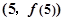 处切线的斜率等于( )
处切线的斜率等于( )
A.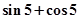 | B.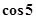 | C.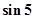 | D.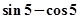 |
曲线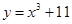 在点
在点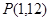 处的切线与
处的切线与 轴交点的纵坐标是( )
轴交点的纵坐标是( )
| A.-9 | B.-3 | C.9 | D.15 |
已知函数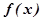 =
= ,
,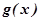 =
=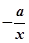 ,若至少存在一个
,若至少存在一个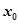 ∈[1,e],使
∈[1,e],使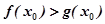 成立,则实数a的范围为( ).
成立,则实数a的范围为( ).
| A.[1,+∞) | B.(0,+∞) | C.[0,+∞) | D.(1,+∞) |
若函数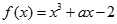 在区间
在区间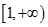 内是增函数,则实数
内是增函数,则实数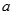 的取值范围是( )
的取值范围是( )
A.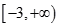 | B.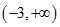 | C.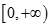 | D.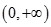 |
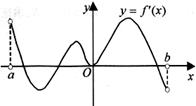
在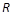 上可导的函数
上可导的函数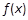 的图形如图所示,
的图形如图所示,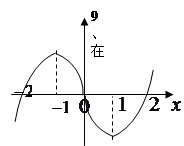 则关于
则关于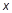 的不等式
的不等式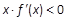 的解集为( ).
的解集为( ).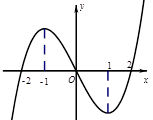
A.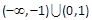 | B.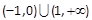 |
C.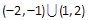 | D. |
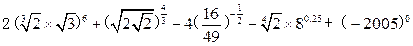
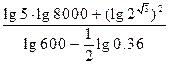 。
。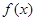 的定义域为开区间
的定义域为开区间 ,其导函数
,其导函数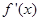 在
在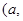
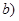 内极小值点的个数为( )
内极小值点的个数为( )