题目内容
已知数列{an}的前n项和Sn=n2(n∈N*),等比数列{bn}满足b1=a1,2b3=b4.
(1)求数列{an}和{bn}的通项公式;
(2)若cn=an·bn(n∈N*),求数列{cn}的前n项和Tn.
(1)bn=2n-1(n∈N*).(2)(2n-3)×2n+3.
【解析】(1)∵当n=1时,a1=S1=1;
当n≥2时,an=Sn-Sn-1=n2-(n-1)2=2n-1,
∴an=2n-1(n∈N*),
∴b1=a1=1,设等比数列{bn}的公比为q,则q≠0.
∵2b3=b4,∴2q2=q3,∴q=2,
∴bn=2n-1(n∈N*).
(2)由(1)可得cn=an·bn=(2n-1)×2n-1(n∈N*),
∴Tn=1×20+3×2+5×22+…+(2n-1)×2n-1,①
∴2Tn=1×2+3×22+5×23+…+(2n-1)×2n,②
②-①得
Tn=(2n-1)×2n-(1×20+2×2+2×22+…+2×2n-1)
=(2n-1)×2n-(1+22+23+…+2n)=(2n-3)×2n+3.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
某农场给某种农作物施肥量x(单位:吨)与其产量y(单位:吨)的统计数据如下表:
施肥量x | 2 | 3 | 4 | 5 |
产量y | 26 | 39 | 49 | 54 |
根据上表,得到回归直线方程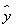 =9.4x+
=9.4x+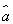 ,当施肥量x=6时,该农作物的预报产量是________.
,当施肥量x=6时,该农作物的预报产量是________.