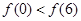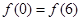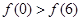题目内容
已知曲线 y = x3 + x-2 在点 P0 处的切线 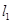 平行直线
平行直线
4x-y-1=0,且点 P0 在第三象限,
求P0的坐标; ⑵若直线 , 且 l 也过切点P0 ,求直线l的方程.
, 且 l 也过切点P0 ,求直线l的方程.
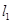 平行直线
平行直线4x-y-1=0,且点 P0 在第三象限,
求P0的坐标; ⑵若直线
 , 且 l 也过切点P0 ,求直线l的方程.
, 且 l 也过切点P0 ,求直线l的方程.(1)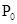 的坐标为
的坐标为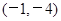 ⑵
⑵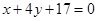
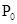 的坐标为
的坐标为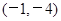 ⑵
⑵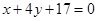
试题分析:(1)根据曲线方程求出导函数,因为已知直线
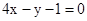 的斜率为4,根据切线与已知直线平行得到斜率相等都为4,所以令导函数等于4得到关于x的方程,求出方程的解,即为切点
的斜率为4,根据切线与已知直线平行得到斜率相等都为4,所以令导函数等于4得到关于x的方程,求出方程的解,即为切点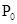 的横坐标,代入曲线方程即可求出切点的纵坐标,又因为切点在第3象限,进而写出满足题意的切点的坐标;
的横坐标,代入曲线方程即可求出切点的纵坐标,又因为切点在第3象限,进而写出满足题意的切点的坐标;(2)由直线l1的斜率为4,根据两直线垂直时斜率的乘积为-1,得到直线l的斜率为
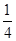 -,又根据(1)中求得的切点坐标,写出直线l的方程即可.
-,又根据(1)中求得的切点坐标,写出直线l的方程即可.⑴由
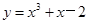 ,得
,得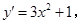
由已知得
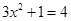 ,解之得
,解之得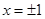 .当
.当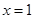 时,
时,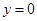 ;当
;当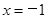 时,
时,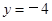 .
.又∵点
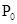 在第三象限,
在第三象限,∴切点
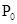 的坐标为
的坐标为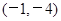 .
.⑵∵直线
 ,
,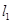 的斜率为4,∴直线l的斜率为
的斜率为4,∴直线l的斜率为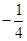 ,
,∵l过切点
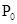 ,点
,点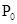 的坐标为
的坐标为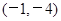 )
)∴直线l的方程为
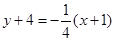 即
即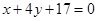 .
.
练习册系列答案
相关题目
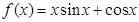 的导函数原点处的部分图象大致为 ( )
的导函数原点处的部分图象大致为 ( )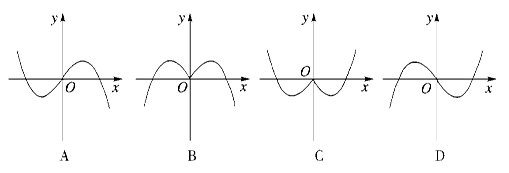
 ,当x∈(-2,0)时,f(x)的最小值为1,则a的值等于________.
,当x∈(-2,0)时,f(x)的最小值为1,则a的值等于________.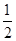 x-
x-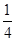 sinx-
sinx-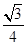 cosx的图象在点A(x0,y0)处的切线斜率为1,则tanx0=________.
cosx的图象在点A(x0,y0)处的切线斜率为1,则tanx0=________.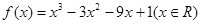 .
.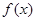 在点
在点 处的切线方程;
处的切线方程;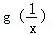 的大小关系;
的大小关系; 对任意x>0成立.
对任意x>0成立.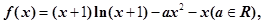
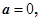 求函数
求函数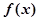 的极值点及相应的极值;
的极值点及相应的极值;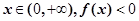 恒成立,求实数
恒成立,求实数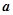 的取值范围.
的取值范围.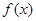 在R上可导,且
在R上可导,且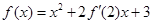 ,则( )
,则( )