题目内容
已知函数f(x)＝3x，且f(a＋2)＝18，g(x)＝3ax－4x的定义域为区间[－1,1]．
(1)求g(x)的解析式；
(2)判断g(x)的单调性．
【答案】
(1)∵f(a＋2)＝18，f(x)＝3x.
∴3a＋2＝18，即3a＝2.
故g(x)＝(3a)x－4x＝2x－4x，x∈[－1,1]．
(2)g(x)＝－(2x)2＋2x＝－2＋.
当x∈[－1,1]时，2x∈.令t＝2x，
由二次函数单调性得
－2＋在上是减函数，
∴函数g(x)在[－1,1]上是减函数．
【解析】略
练习册系列答案
相关题目
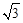sin ax cos ax＋2 cos2 ax的周期为π，其中a＞0．
sin
ax cos ax＋2 cos2 ax的周期为π，其中a＞0．
的最大值；
)>kg(x)对x∈[2,4]有解，求实数k的取值范围．
sin
ax cos ax＋2 cos2 ax的周期为π，其中a＞0．
，无最小值