题目内容
已知函数f(x)=3-2log2x,g(x)=log2x.
(1)如果x∈[1,4],求函数h(x)=(f(x)+1)g(x)的值域;
(2)求函数M(x)= 的最大值;
的最大值;
(3)如果不等式f(x2)f( )>kg(x)对x∈[2,4]有解,求实数k的取值范围.
)>kg(x)对x∈[2,4]有解,求实数k的取值范围.
【答案】
(1)[0,2].(2)当x=2时,M(x)取到最大值为1.
(3)k<-2.
【解析】
试题分析:(1)h(x)=(4-2log2x)·log2x=-2(log2x-1)2+2,
∵x∈[1,4],∴log2x∈[0,2],
∴h(x)的值域为[0,2].
(2):f(x)-g(x)=3(1-log2x).
当x>2时,f(x)<g(x);当0<x≤2时,f(x)≥g(x).
∴M(x)= =
=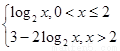
当0<x≤2时,M(x)最大值为1;
当x>2时,M(x)<1;
综上:当x=2时,M(x)取到最大值为1.
(3)由f(x2)f(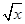 )>kg(x)得
)>kg(x)得
(3-4log2x)(3-log2x)>k·log2x,
令t=log2x,∵x∈[2,4],∴t∈1,2],∴存在t∈[1,2]使(3-4t)(3-t)>kt,
即k< = 4t+
= 4t+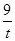 -15成立
-15成立
记h (x) = 4t+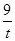 -15,则k< h (x)max即可,易得h
(x)max=-2
-15,则k< h (x)max即可,易得h
(x)max=-2
综上:k<-2.
考点:函数的最值
点评:解决的管家式利用对数式的运算,以及函数的性质,均值不等式来求解最值,属于中档题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
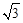 sin ax cos ax+2 cos2 ax的周期为π,其中a>0.
sin ax cos ax+2 cos2 ax的周期为π,其中a>0. sin
ax cos ax+2 cos2 ax的周期为π,其中a>0.
sin
ax cos ax+2 cos2 ax的周期为π,其中a>0. sin
ax cos ax+2 cos2 ax的周期为π,其中a>0.
sin
ax cos ax+2 cos2 ax的周期为π,其中a>0. ,无最小值
,无最小值