题目内容
已知函数f (x)=3 sin2 ax+ sin
ax cos ax+2 cos2 ax的周期为π,其中a>0.
sin
ax cos ax+2 cos2 ax的周期为π,其中a>0.
(Ⅰ) 求a的值;
(Ⅱ) 求f (x)的值域.
【答案】
(Ⅰ)a=1.(Ⅱ) f (x)的值域为[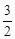 ,
,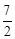 ].
].
【解析】
试题分析:(Ⅰ) 由题意得
f (x)=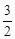 (1-cos 2ax)+
(1-cos 2ax)+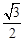 sin
2ax+(1+cos 2ax)
sin
2ax+(1+cos 2ax)
=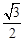 sin
2ax-
sin
2ax-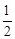 cos
2ax+
cos
2ax+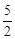
=sin (2ax-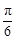 )+
)+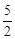 .
.
因为f (x)的周期为π,a>0,所以a=1.
(Ⅱ) 由(Ⅰ)得
f (x)=sin (2x-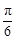 )+
)+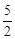 ,
,
所以f (x)的值域为[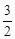 ,
,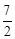 ].
].
考点:三角恒等变换,三角函数最值
点评:本题主要考查三角函数的图象与性质、三角变换等基础知识,同时考查运算求解能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 )x有两个零点x1,x2,则有
)x有两个零点x1,x2,则有