题目内容
【题目】如图,四棱锥E﹣ABCD的侧棱DE与四棱锥F﹣ABCD的侧棱BF都与底面ABCD垂直,![]() ,
,![]() //
//![]() ,
,![]() .
.
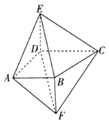
(1)证明:![]() //平面BCE.
//平面BCE.
(2)设平面ABF与平面CDF所成的二面角为θ,求![]() .
.
【答案】(1)证明见解析(2)![]()
【解析】
(1)根据线面垂直的性质定理,可得DE//BF,然后根据勾股定理计算可得BF=DE,最后利用线面平行的判定定理,可得结果.
(2)利用建系的方法,可得平面ABF的一个法向量为![]() ,平面CDF的法向量为
,平面CDF的法向量为![]() ,然后利用向量的夹角公式以及平方关系,可得结果.
,然后利用向量的夹角公式以及平方关系,可得结果.
(1)因为DE⊥平面ABCD,所以DE![]() AD,
AD,
因为AD=4,AE=5,DE=3,同理BF=3,
又DE⊥平面ABCD,BF⊥平面ABCD,
所以DE//BF,又BF=DE,
所以平行四边形BEDF,故DF//BE,
因为BE![]() 平面BCE,DF
平面BCE,DF![]() 平面BCE
平面BCE
所以DF//平面BCE;
(2)建立如图空间直角坐标系,
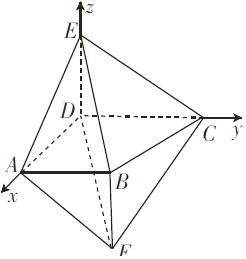
则D(0,0,0),A(4,0,0),
C(0,4,0),F(4,3,﹣3),
![]() ,
,
设平面CDF的法向量为![]() ,
,
由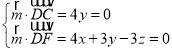 ,令x=3,得
,令x=3,得![]() ,
,
易知平面ABF的一个法向量为![]() ,
,
所以![]() ,
,
故![]() .
.

练习册系列答案
相关题目