题目内容
(文科)设曲线 在点(1,1)处的切线与x轴的交点的横坐标为
在点(1,1)处的切线与x轴的交点的横坐标为 ,
, = ,令
= ,令 ,则
,则 的值为 .
的值为 .
 在点(1,1)处的切线与x轴的交点的横坐标为
在点(1,1)处的切线与x轴的交点的横坐标为 ,
, = ,令
= ,令 ,则
,则 的值为 .
的值为 . 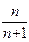 ,-2
,-2函数 的导数为
的导数为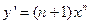 ,故在点
,故在点 处的切线方程为
处的切线方程为 ,令
,令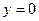 ,则
,则 。
。
 。
。
 的导数为
的导数为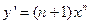 ,故在点
,故在点 处的切线方程为
处的切线方程为 ,令
,令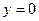 ,则
,则 。
。
 。
。
练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
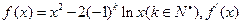 表示f(x)导函数。
表示f(x)导函数。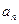 }满足
}满足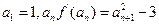 .证明:数列{
.证明:数列{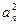 }中
}中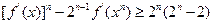 成立.
成立.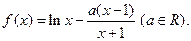
 数
数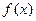 在其定义域内是增函数,求
在其定义域内是增函数,求 的取值范围;
的取值范围; ,方程
,方程 有两根
有两根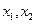 ,记
,记 .试探究
.试探究 值的符号,其中
值的符号,其中 是
是 的导函数.
的导函数.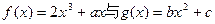 的图像都过点P(2,0),且在点P处
的图像都过点P(2,0),且在点P处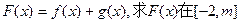 上的最小值。
上的最小值。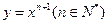 在点(1,1)处的切线与x轴的交点的横坐标为
在点(1,1)处的切线与x轴的交点的横坐标为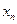 ,令
,令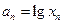 ,则
,则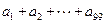 的值为 。
的值为 。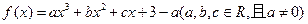 ,当
,当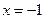 时,
时, 取到极大值2。
取到极大值2。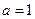 时,求
时,求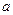 的取值范围。
的取值范围。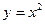 在
在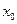 到
到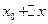 的平均变化率为
的平均变化率为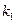 ,在
,在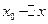 到
到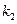 ,则二者的大小关系是 .
,则二者的大小关系是 .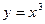 的极值点;
的极值点;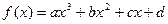 有极值点的充要条件是
有极值点的充要条件是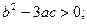
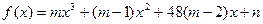 在区间(-4,4)上是单调减函数.
在区间(-4,4)上是单调减函数.