题目内容
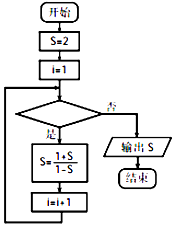
【题目】已知递增数列{an}，a1=2，其前n项和为Sn ， 且满足3（Sn+Sn﹣1）= 
+2（n≥2）．
（1）求数列{an}的通项公式；
（2）若数列{bn}满足 
=n，求其前n项和Tn ．
【答案】
（1）解：3（Sn+Sn﹣1）= 
+2（n≥2），
可得3（Sn﹣1+Sn﹣2）=an﹣12+2（n≥3）．
两式相减可得3（an+an﹣1）=（an+an﹣1）（an﹣an﹣1），
由递增数列{an}，a1=2，
可得an﹣an﹣1=3，（n≥3）．
由3（a1+a2+a1）=a22+2，3（a1+a2+a3+a1+a2）=a32+2，
求得a2=5，a3=8，
由等差数列的通项公式可得an=8+3（n﹣3）=3n﹣1，
上式对n=1，2也成立，
故数列{an}的通项公式为an=3n﹣1；
（2）解：数列{bn}满足 
=n，
可得bn=（3n﹣1）2n，
前n项和Tn=22+522+823+…+（3n﹣1）2n，
2Tn=222+523+824+…+（3n﹣1）2n+1，
两式相减可得，﹣Tn=4+3（22+23+…+2n）﹣（3n﹣1）2n+1
=4+3 
﹣（3n﹣1）2n+1，
化简可得Tn=（3n﹣4）2n+1+8
【解析】（1）运用数列的递推式，n≥2时，an=Sn﹣Sn﹣1 ， 结合条件和等差数列的定义和通项公式即可得到所求；（2）求出bn=（3n﹣1）2n ， 运用数列的求和方法：错位相减法，结合等比数列的求和公式，化简整理，即可得到所求和．
【考点精析】解答此题的关键在于理解数列的前n项和的相关知识，掌握数列{an}的前n项和sn与通项an的关系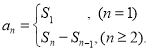
，以及对数列的通项公式的理解，了解如果数列an的第n项与n之间的关系可以用一个公式表示，那么这个公式就叫这个数列的通项公式．
【题目】调查表明：甲种农作物的长势与海拔高度、土壤酸碱度、空气湿度的指标有极强的相关性，现将这三项的指标分别记为x，y，z，并对它们进行量化：0表示不合格，1表示临界合格，2表示合格，再用综合指标ω=x+y+z的值评定这种农作物的长势等级，若ω≥4，则长势为一级；若2≤ω≤3，则长势为二级；若0≤ω≤1，则长势为三级，为了了解目前这种农作物长势情况，研究人员随机抽取10块种植地，得到如表中结果：
种植地编号 | A1 | A2 | A3 | A4 | A5 |
（x，y，z） | （1，1，2） | （2，1，1） | （2，2，2） | （0，0，1） | （1，2，1） |
种植地编号 | A6 | A7 | A8 | A9 | A10 |
（x，y，z） | （1，1，2） | （1，1，1） | （1，2，2） | （1，2，1） | （1，1，1） |
（Ⅰ）在这10块该农作物的种植地中任取两块地，求这两块地的空气湿度的指标z相同的概率；
（Ⅱ）从长势等级是一级的种植地中任取一块地，其综合指标为A，从长势等级不是一级的种植地中任取一块地，其综合指标为B，记随机变量X=A﹣B，求X的分布列及其数学期望．