Question

【题目】如图，在三棱锥 中，平面 平面 ， 为等边三角形， 且 ， 分别为 的中点.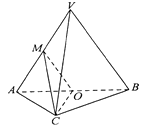

（1）求证： 平面 .
（2）求证：平面 平面 .
（3）求三棱锥 的体积.

Answer 1

【答案】
（1）解：因为 分别是 的中点，
所以 ，
因为 面 ， 平面 ，
所以 平面
（2）解： ， 是 的中点，
所以 ，
又因为平面 平面 ，且 平面 ，
所以 平面 ，所以平面 平面
（3）解：在等腰直角三角形 中， ，
所以 ， ，
所以等边三角形 的面积 ，
又因为 平面 ，
所以三棱锥 的体积等于 .
又因为三棱锥 的体积与三棱锥 的体积相等
【解析】（1）根据中位线定理证明VB//OM，进而证明直线VB//平面MOC。
（2）等边三角形中，斜边中线即为高线，证明AB与OC垂直，利用已知条件中的面面垂直，证明OC与平面VAB垂直，利用面面垂直的判定定理证明结论。
（3）利用等体积法，将三棱锥V-ABC的体积转化为求三棱锥C-VAB的体积，利用（2）的结论求出结果。