题目内容
5.已知an=logn+1(n+2)(n∈N*),观察下列运算a1•a2=log23•log34=$\frac{lg3}{lg2}$•$\frac{lg4}{lg3}$=2,a1•a2•a3•a4•a5•a6=log23•log34•…•log67•log78=$\frac{lg3}{lg2}$•$\frac{lg4}{lg3}$•…•$\frac{lg7}{lg6}$•$\frac{lg8}{lg7}$=3.定义使a1•a2•a3•…•ak为整数的k(k∈N*)叫做企盼数.则区间[1,2016]内的所有企盼数的和为 ( )| A. | 2026 | B. | 2057 | C. | 2073 | D. | 2074 |
分析 利用对数的运算性质可知a1•a2•a3•…•ak=$\frac{lg(k+2)}{lg2}$,进而计算可得结论.
解答 解:∵an=logn+1(n+2)(n∈N*),
∴a1•a2•a3•…•ak=$\frac{lg3}{lg2}$•$\frac{lg4}{lg3}$•…•$\frac{lg(k+1)}{lgk}$•$\frac{lg(k+2)}{lg(k+1)}$=$\frac{lg(k+2)}{lg2}$,
∴k+2=2t(t≥2,t∈N*),
于是区间[1,2016]内的所有企盼数的和为(22-2)+(23-2)+…+(210-2)=$\frac{{2}^{2}(1-{2}^{9})}{1-2}$-2×9=2026,
故选:A.
点评 本题考查数列的通项,考查运算求解能力,利用对数的性质是解决本题的关键,注意解题方法的积累,属于中档题.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
13.设|$\overrightarrow{AB}$|=2,|$\overrightarrow{AC}$|=3,∠BAC=60°,$\overrightarrow{CD}$=2$\overrightarrow{BC}$,$\overrightarrow{AE}$=x$\overrightarrow{AD}$+(1-x)$\overrightarrow{AB}$,x∈[0,1],则$\overrightarrow{AE}$在$\overrightarrow{AC}$上的投影的取值范围是( )
| A. | [0,1] | B. | [1,7] | C. | [7,9] | D. | [9,21] |
20.下列函数中,以π为周期的函数是( )
| A. | y=|sinx| | B. | y=sin|x| | C. | y=sinx | D. | y=$\frac{1}{2}$sinx |
14.在等差数列{an}中,a9=$\frac{1}{2}$a12+6,a2=4,设数列{an}的前n项和为Sn,则数列{$\frac{1}{{S}_{n}}$}的前10项和为( )
| A. | $\frac{11}{12}$ | B. | $\frac{10}{11}$ | C. | $\frac{9}{10}$ | D. | $\frac{8}{9}$ |
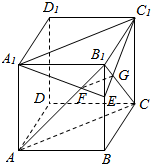 如图,在正方体ABCD-A1B1C1D1中,E为BB1上不同于B、B1的任一点,AB1∩A1E=F,B1C∩C1E=G.
如图,在正方体ABCD-A1B1C1D1中,E为BB1上不同于B、B1的任一点,AB1∩A1E=F,B1C∩C1E=G.