题目内容
已知椭圆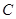 :
: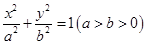 的离心率为
的离心率为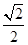 ,左焦点为
,左焦点为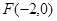 .
.
(Ⅰ)求椭圆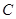 的方程;
的方程;
(Ⅱ)若直线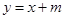 与曲线
与曲线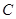 交于不同的
交于不同的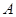 、
、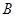 两点,且线段
两点,且线段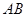 的中点
的中点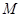 在圆
在圆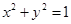 上,求
上,求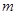 的值.
的值.
【答案】
(Ⅰ) ;(Ⅱ)
;(Ⅱ) .
.
【解析】
试题分析:(Ⅰ)利用离心率和直线与焦点坐标得到两个等量关系,确定椭圆方程;(Ⅱ)利用直线与圆联立,借助韦达定理和中点坐标M在圆上建立等量关系.
试题解析:(Ⅰ)由题意得 ,
, 2分
2分
解得 4分
4分
所以椭圆C的方程为: 6分
6分
(Ⅱ)设点 、
、 的坐标分别为
的坐标分别为 ,
, ,线段
,线段 的中点为
的中点为 ,
,
由 ,消去y得
,消去y得 8分
8分
∵ ,∴
,∴ 9分
9分
∴ ,
, 10分
10分
∵点  在圆
在圆 上,∴
上,∴ ,即
,即 13分
13分
考点:1.椭圆方程;2.直线与圆的位置关系.

练习册系列答案
相关题目
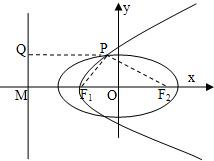 已知椭圆E的离心率为e,两焦点为F1,F2,抛物线C以F1为顶点,F2为焦点,P为两曲线的一个公共点,若
已知椭圆E的离心率为e,两焦点为F1,F2,抛物线C以F1为顶点,F2为焦点,P为两曲线的一个公共点,若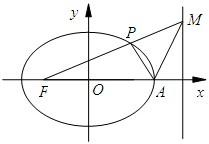 如图,在平面直角坐标系xOy中,椭圆C:
如图,在平面直角坐标系xOy中,椭圆C: