题目内容
已知椭圆C的离心率为e=
,一条准线方程为x=
.
(1)求椭圆C的标准方程;
(2)设动点P满足:
=
+
,其中M,N是椭圆上的点,直线OM与ON的斜率之积为-
,问:是否存在两个定点A,B,使得|PA|+|PB|为定值?若存在,求A,B的坐标;若不存在,说明理由.
| ||
| 3 |
3
| ||
| 2 |
(1)求椭圆C的标准方程;
(2)设动点P满足:
| OP |
| OM |
| ON |
| 1 |
| 3 |
分析:(1)设出椭圆的标准方程,利用椭圆C的离心率为e=
,一条准线方程为x=
,建立方程组,求得几何量,即可求椭圆C的标准方程;
(2)利用
=
+
,直线OM与ON的斜率之积为-
,确定P的轨迹方程,即可求得结论.
| ||
| 3 |
3
| ||
| 2 |
(2)利用
| OP |
| OM |
| ON |
| 1 |
| 3 |
解答:解:(1)设椭圆的标准方程为:
+
=1(a>b>0)
∵椭圆C的离心率为e=
,一条准线方程为x=
∴
,∴a=
,c=
,∴b=1
∴椭圆C的标准方程为
+y2=1; ….(4分)
(2)设P(x,y),M(x1,y1),N(x2,y2),则由
=
+
得x=x1+x2,y=y1+y2…(6分)
因为点M,N在椭圆
+y2=1上,即x2+3y2=3,所以x12+3y12=3,x22+3y22=3…(8分)
故x2+3y2=(x1+x2)2+3(y1+y2)2=(x12+3y12)+(x22+3y22)+2(x1x2+3y1y2)=6+2(x1x2+3y1y2)…(10分)
设分别为直线OM,ON的斜率,由题设条件知kOM•kON=
=-
,因此x1x2+3y1y2=0…(12分)
所以x2+3y2=6,即
+
=1….(14分)
所以P点是椭圆
+
=1上的点,设该椭圆的左、右焦点为A,B,则由椭圆的定义|PA|+|PB|为定值,又因c=
=2,因此两焦点的坐标为A(-2,0),B(2,0). …(16分)
| x2 |
| a2 |
| y2 |
| b2 |
∵椭圆C的离心率为e=
| ||
| 3 |
3
| ||
| 2 |
∴
|
| 3 |
| 2 |
∴椭圆C的标准方程为
| x2 |
| 3 |
(2)设P(x,y),M(x1,y1),N(x2,y2),则由
| OP |
| OM |
| ON |
因为点M,N在椭圆
| x2 |
| 3 |
故x2+3y2=(x1+x2)2+3(y1+y2)2=(x12+3y12)+(x22+3y22)+2(x1x2+3y1y2)=6+2(x1x2+3y1y2)…(10分)
设分别为直线OM,ON的斜率,由题设条件知kOM•kON=
| y1y2 |
| x1x2 |
| 1 |
| 3 |
所以x2+3y2=6,即
| x2 |
| 6 |
| y2 |
| 2 |
所以P点是椭圆
| x2 |
| 6 |
| y2 |
| 2 |
| 6-2 |
点评:本题考查椭圆的几何性质,考查标准方程,考查向量知识的运用,考查学生分析解决问题的能力,确定椭圆的标准方程是关键.

练习册系列答案
相关题目
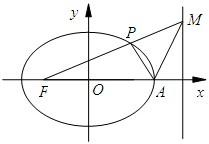 如图,在平面直角坐标系xOy中,椭圆C:
如图,在平面直角坐标系xOy中,椭圆C: 如图所示,已知椭圆C的离心率为
如图所示,已知椭圆C的离心率为 的离心率为
的离心率为 ,以原点为圆心,椭圆的短半轴长为半径的圆与直线
,以原点为圆心,椭圆的短半轴长为半径的圆与直线 相切.
相切. 的方程;
的方程; (2,0)的直线与椭圆
(2,0)的直线与椭圆 ,设
,设 为椭圆上一点,且满足
为椭圆上一点,且满足 (
( 为坐标原点),当
为坐标原点),当 时,求实数
时,求实数 取值范围.
取值范围.