题目内容
【题目】已知函数![]()
(1)当![]() 时,求函数
时,求函数![]() 的极值;
的极值;
(2)若函数![]() 在区间
在区间![]() 内存在零点,求实数
内存在零点,求实数![]() 的取值范围.
的取值范围.
【答案】(1) 极小值为![]() ,无极大值;(2)
,无极大值;(2) ![]() .
.
【解析】
(1)![]() ,可求
,可求![]() ,则
,则![]() ,可判断
,可判断![]() 时,
时,![]() 单调递减;
单调递减; ![]() 时,
时, ![]() 单调递增,即可求得
单调递增,即可求得![]() 在
在![]() 处取得极小值,无极大值.
处取得极小值,无极大值.
(2)函数![]() 在区间
在区间![]() 内存在零点等价于
内存在零点等价于![]() 在
在![]() 内有解,通过讨论
内有解,通过讨论![]() ,
,![]() ,
,![]() ,三种情况下求
,三种情况下求![]() 的最值及单调情况即可.
的最值及单调情况即可.
(1)若![]() ,则
,则![]() ,
,![]() ,则
,则![]() ,
,
当![]() 时,
时, ![]() 单调递减; 当
单调递减; 当![]() 时,
时, ![]() 单调递增,所以
单调递增,所以![]() 在
在![]() 处取得极小值,且极小值为
处取得极小值,且极小值为![]() ,无极大值.
,无极大值.
(2)由题意![]() ,设
,设![]() ,则
,则![]() .
.
若![]() ,则
,则![]() ,故由(1)得
,故由(1)得![]() 在区间
在区间![]() 内没有零点.
内没有零点.
若![]() ,则
,则![]() ,故
,故![]() 在区间
在区间![]() 内单调递增.又
内单调递增.又![]() ,所以存在
,所以存在![]() ,使
,使![]() ,故当
,故当![]() 时,
时, ![]() 单调递减; 当
单调递减; 当![]() 时,
时, ![]() 单调递增.因为
单调递增.因为![]() ,所以当
,所以当![]() 时,
时, ![]() 在区间
在区间![]() 内存在零点.
内存在零点.
若![]() ,由(1)得当
,由(1)得当![]() 时,
时, ![]() .则
.则![]()
此函数![]() 在区间
在区间![]() 内没有零点.
内没有零点.
综上, 实数![]() 的取值范围
的取值范围![]()

 优学名师名题系列答案
优学名师名题系列答案【题目】垃圾种类可分为可回收垃圾,干垃圾,湿垃圾,有害垃圾,为调查中学生对垃圾分类的了解程度某调查小组随机抽取了某市的100名高中生,请他们指出生活中若干项常见垃圾的种类,把能准确分类不少于3项的称为“比较了解”少于三项的称为“不太了解”调查结果如下:
0项 | 1项 | 2项 | 3项 | 4项 | 5项 | 5项以上 | |
男生(人) | 1 | 10 | 17 | 14 | 14 | 10 | 4 |
女生(人) | 0 | 8 | 10 | 6 | 3 | 2 | 1 |
(1)完成如下![]() 列联表并判断是否有95%的把握认为了解垃圾分类与性别有关?
列联表并判断是否有95%的把握认为了解垃圾分类与性别有关?
比较了解 | 不太了解 | 合计 | |
男生 | __________ | __________ | __________ |
女生 | __________ | __________ | __________ |
合计 | __________ | __________ | __________ |
(2)从能准确分类不少于3项的高中生中,按照男、女生采用分层抽样的方法抽取9人的样本.
(i)求抽取的女生和男生的人数;
(ii)从9人的样本中随机抽取两人,求男生女生都有被抽到的概率.
参考数据:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
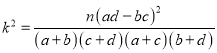 ,
,![]() .
.