题目内容
|
如图,正方体 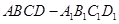 中,点 中,点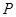 在 在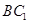 上运动,给出下列四个命题: 上运动,给出下列四个命题: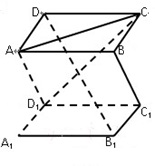 ①三棱锥 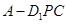 的体积不变; ② 的体积不变; ②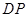 ⊥ ⊥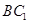 ; ;③ 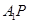 ∥平面 ∥平面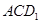 ; ④平面 ; ④平面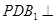 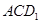 ; ;其中正确的命题个数有( )
|
C
分析: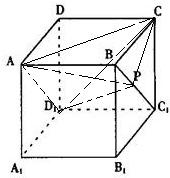 ①V A-D1PC=V C-AD1P,C到面 AD1P的距离不变,且三角形 AD1P的面积不变.
①V A-D1PC=V C-AD1P,C到面 AD1P的距离不变,且三角形 AD1P的面积不变.
②,当P 与B重合时,DP与BC1;成60°角,不垂直.
③连接A1B,A1C1容易证明平面BA1C1∥面ACD1,从而由线面平行的定义可得;
④连接DB1,容易证明DB1⊥面ACD1 ,从而可以证明面面垂直.
解答: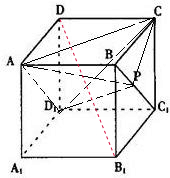 解:对于①,V A-D1PC=V C-AD1P,C到面 AD1P的距离不变,且三角形 AD1P的面积不变.∴三棱锥A-D1PC的体积不变; 正确;
解:对于①,V A-D1PC=V C-AD1P,C到面 AD1P的距离不变,且三角形 AD1P的面积不变.∴三棱锥A-D1PC的体积不变; 正确;
②连接DB,DC1,可知△DBC1是正三角形,当且仅当P为BC1中点时,DP⊥BC1,考虑特殊位置,当P 与B重合时,DP与BC1成60°角,不垂直.
错误
③连接A1B,A1C1容易证明平面BA1C1∥面ACD1,从而由线面平行的定义可得 A1P∥平面ACD1;.正确.
④连接DB1,根据正方体的性质,有DB1⊥面ACD1 ,DB1?平面PDB1 从而可以证明平面PDB1⊥ACD1;正确.
正确的命题个数有 3个.
故选C.
点评:本题考查三棱锥体积求法中的等体积法;线面平行、垂直,面面平行、垂直的判定,要注意使用转化的思想,及特殊和一般的思想方法.
 ①V A-D1PC=V C-AD1P,C到面 AD1P的距离不变,且三角形 AD1P的面积不变.
①V A-D1PC=V C-AD1P,C到面 AD1P的距离不变,且三角形 AD1P的面积不变.②,当P 与B重合时,DP与BC1;成60°角,不垂直.
③连接A1B,A1C1容易证明平面BA1C1∥面ACD1,从而由线面平行的定义可得;
④连接DB1,容易证明DB1⊥面ACD1 ,从而可以证明面面垂直.
解答:
 解:对于①,V A-D1PC=V C-AD1P,C到面 AD1P的距离不变,且三角形 AD1P的面积不变.∴三棱锥A-D1PC的体积不变; 正确;
解:对于①,V A-D1PC=V C-AD1P,C到面 AD1P的距离不变,且三角形 AD1P的面积不变.∴三棱锥A-D1PC的体积不变; 正确;②连接DB,DC1,可知△DBC1是正三角形,当且仅当P为BC1中点时,DP⊥BC1,考虑特殊位置,当P 与B重合时,DP与BC1成60°角,不垂直.
错误
③连接A1B,A1C1容易证明平面BA1C1∥面ACD1,从而由线面平行的定义可得 A1P∥平面ACD1;.正确.
④连接DB1,根据正方体的性质,有DB1⊥面ACD1 ,DB1?平面PDB1 从而可以证明平面PDB1⊥ACD1;正确.
正确的命题个数有 3个.
故选C.
点评:本题考查三棱锥体积求法中的等体积法;线面平行、垂直,面面平行、垂直的判定,要注意使用转化的思想,及特殊和一般的思想方法.

练习册系列答案
相关题目
 个
个 个
个 个
个 个
个 中.
中.
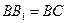 ,
,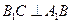 ,证明:平面
,证明:平面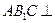 平面
平面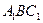 ;
;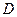 是
是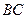 的中点,
的中点,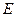 是
是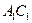 上的一点,
上的一点,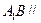 平面
平面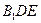 ,求
,求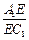 的值.
的值. 平方米的材料制成一个有盖的圆锥形容器,如果在制作过程中材料无损耗,且材料的厚度忽略不计,底面半径长为
平方米的材料制成一个有盖的圆锥形容器,如果在制作过程中材料无损耗,且材料的厚度忽略不计,底面半径长为 ,圆锥母线的长为
,圆锥母线的长为

 ,求所制作的圆锥形容器容积多少立方米(精确到0. 01m3) (6分)
,求所制作的圆锥形容器容积多少立方米(精确到0. 01m3) (6分)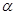 ,那么对于空间内的任意一条直线
,那么对于空间内的任意一条直线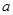 ,在平面
,在平面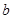 ,使得
,使得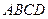 中,
中,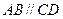 ,
,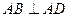 ,且
,且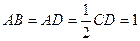 .
.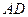 为一边向形外作正方形
为一边向形外作正方形 ,然后沿边
,然后沿边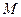 为
为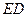 的中点,如图2.
的中点,如图2.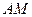 ∥平面
∥平面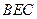 ;
;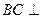 平面
平面 ;
; 到平面
到平面
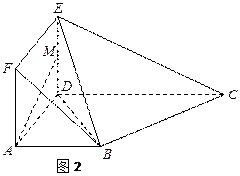
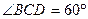 ,E是CD的中点,
,E是CD的中点,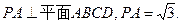
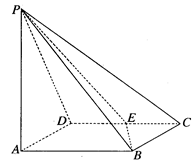
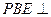 平面PAB;
平面PAB;  中,其中
中,其中 ,
, 外接球球心为点O,外接球体积为
外接球球心为点O,外接球体积为 ,若
,若 的最小值为
的最小值为 ,则
,则 两点的球面距离为 .
两点的球面距离为 .
 ,若
,若 ,且
,且 与
与 相交但不垂直,直线
相交但不垂直,直线 分别为
分别为 ;②任意
;②任意 ; ③存在
; ③存在 ; ④存在
; ④存在 ; ⑤任意
; ⑤任意 ; ⑥存在
; ⑥存在 。真命题的序号是_________ 。
。真命题的序号是_________ 。 是两不同的直线,
是两不同的直线, 是两不同的平面,则下列命题正确的是 ( )
是两不同的平面,则下列命题正确的是 ( )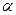 ⊥
⊥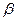 ,
,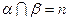 ,
,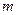 ⊥
⊥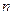 ,则
,则