Question

已知集合M={(x，y)|y=x+m}，N={(x，y)|

x=cosθ y=sinθ

，θ∈[-

π

2

，

π

2

]，若M∩N≠?，则实数m的取值范围是（　　）

• A、(-

  2

  ，-1]
• B、[-

  2

  ，1]
• C、(-

  2

  ，

  2

  )
• D、[1，

  2

  )

Answer 1

分析：求出N中圆的普通方程，利用数形结合，即可求出m的取值范围．

解答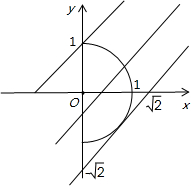：解：N={(x，y)|

x=cosθ y=sinθ

，θ∈[-

π

2

，

π

2

]，
所以N集合的方程x²+y²=1（x∈[0，1]）
如图，若M∩N≠?，所以m∈[-

2

，1]．
故选B．

点评：本题是基础题，考查圆的参数方程与普通方程的互化，数形结合的解题思想，常考题型，注意角的范围的应用．