题目内容
如图,已知四棱锥P-ABCD,底面是边长为2的正方形,侧棱PA⊥底面ABCD,且PA=2,E为AB的中点.
(Ⅰ)求证二面角E-PC-D为直二面角;
(Ⅱ)求点D到面PEC的距离.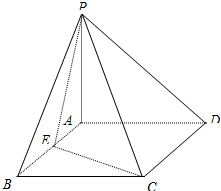
(Ⅰ)求证二面角E-PC-D为直二面角;
(Ⅱ)求点D到面PEC的距离.

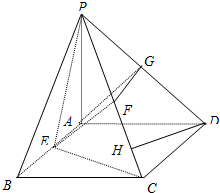
(Ⅰ)取PC、PD的中点F、G,连接EF、FG、AG.
∵PA⊥面ABCD,CD?面ACBD,
∴PA⊥CD,
∵AD⊥CD,PA∩AD=A,∴CD⊥面PAD,
又∵AG?面PAD,∴CD⊥AG.(2分)
∵AG是等腰Rt△PAD斜边PD上的中线,
∴AG⊥PD,(3分)
∴结合 PD∩AD=D,可得AG⊥面PCD.(4分)
∵FG是△PCD的中位线,
∴FG∥CD且FG=
| 1 |
| 2 |
又∵平行四边形ABCD中,AE∥CD且AE=
| 1 |
| 2 |
∴FG
| ∥ |
| . |
∴EF∥AG,(6分)
∴EF⊥面PCD,(7分)
又∵EF?面PEC,∴面PEC⊥面PCD,
即二面角E-PC-D为直二面角.(8分)
(Ⅱ)如图,在RT△PCD中DH⊥PD,垂足为H.
∵面PEC⊥面PCD,且DH垂直于它们的交线,
∴DH⊥面PCE,即DH的长度为点D到面PEC的距离.(10分)
在RT△PCD中,CD=2,PD=2
| 2 |
| 3 |
∴DH=
| CD×PD |
| PC |
2×2
| ||
2
|
2
| ||
| 3 |
即点D到面PEC的距离
2
| ||
| 3 |

练习册系列答案
相关题目
 如图:已知四棱锥P-ABCD中,PD⊥平面ABCD,ABCD是正方形,E是PA的中点,
如图:已知四棱锥P-ABCD中,PD⊥平面ABCD,ABCD是正方形,E是PA的中点, 如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点.
如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点. 如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=60°,PD⊥AD.点E是BC边上的中点.
如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=60°,PD⊥AD.点E是BC边上的中点. (2012•崇明县二模)如图,已知四棱锥P-ABCD的底面ABCD为正方形,PA⊥平面ABCD,E、F分别是BC,PC的中点,AB=2,AP=2.
(2012•崇明县二模)如图,已知四棱锥P-ABCD的底面ABCD为正方形,PA⊥平面ABCD,E、F分别是BC,PC的中点,AB=2,AP=2. (2012•吉林二模)如图,已知四棱锥P-ABCD的底面是正方形,PA⊥面ABCD,且PA=AD=2,点M,N分别在PD,PC上,
(2012•吉林二模)如图,已知四棱锥P-ABCD的底面是正方形,PA⊥面ABCD,且PA=AD=2,点M,N分别在PD,PC上,