题目内容
10.关于x的方程x2+x+p=0(p∈R)至少存在一个根x0,若|x0|=1,则p=-2或0或1.分析 分x0为实数和虚数两种情况求解,当x0为实数时,直接代入球p,当x0为虚数时,由|x0|=1,借助于1的立方虚根求得p值.
解答 解:当x0∈R 时,
由|x0|=1,得x0=±1,
若x0=1,则1+1+p=0,即p=-2,此时方程x2+x+p=0化为方程x2+x-2=0,有两实数根;
若x0=-1,则(-1)2-1+p=0,即p=0,此时方程x2+x+p=0化为方程x2+x=0,有两实数根;
当x0为虚数时,
若关于x的方程x2+x+p=0(p∈R)至少存在一个根x0,且|x0|=1,
则x0为1的一个立方虚根,由此可知p=1.
故答案为:-2或0或1.
点评 本题考查实系数一元二次方程根的问题,考查了代入法,是基础题.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
15.某一几何体的三视图如图所示,按照给出的尺寸(单位:cm),则这个几何体的体积为( )
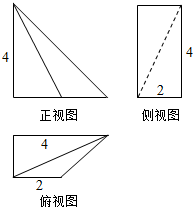

| A. | 8cm3 | B. | $\frac{40}{3}$cm3 | C. | 12cm3 | D. | $\frac{50}{3}$cm3 |
20.下列命题中正确的是( )
| A. | 若a,b,c成等差数列,则a2,b2,c2成等差数列 | |
| B. | 若a,b,c成等差数列,则log2a,log2b,log2c成等差数列 | |
| C. | 若a,b,c成等差数列,则a+2,b+2,c+2成等差数列 | |
| D. | 若a,b,c成等差数列,则2a,2b,2c成等差数列 |