题目内容
设函数f(x)=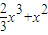 +ax+b(x>-1).
+ax+b(x>-1).(I)若函数f(x)在其定义域上是单调函数,求实数a的取值范围;
(II)若函数f(x)在其定义域上既有极大值又有极小值,求实数a的取值范围.
【答案】分析:(I)由f(x)的解析式求出导函数,导函数为开口向上的抛物线,因为函数在(-1,+∞)上为单调函数,所以导函数与x轴没有交点,列出关于a的不等式,求出不等式的解集即可得到实数a的取值范围.
(II)先对函数进行求导,根据函数f(x)既有极大值又有极小值,可以得到△>0且f′(-1)>0,进而可解出a的范围.
解答:解:(I)由f(x)= +ax+b(x>-1).
+ax+b(x>-1).
得到f′(x)=2x2+2x+a,
因为函数在(-1,+∞)上是单调函数,
所以f′(x)=2x2+2x+a≤0在(-1,+∞)恒成立,由于抛物线开口向上,2x2+2x+a≤0不可能成立;
所以f′(x)=2x2+2x+a≥0在(-1,+∞)恒成立,
则a≥-2x2-2x⇒a≥
所以实数a的取值范围是:[ ,+∞).
,+∞).
(II)∵函数f(x)既有极大值又有极小值
由题意f′(x)=2x2+2x+a=0在(-1,+∞)上有两解,
∴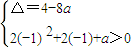 ⇒0<a<
⇒0<a<
故实数a的取值范围0<a< .
.
点评:此题考查函数在某点取得极值的条件、考查学生会利用导函数的正负确定函数的单调区间,掌握函数恒成立时所取的条件,是一道综合题.
(II)先对函数进行求导,根据函数f(x)既有极大值又有极小值,可以得到△>0且f′(-1)>0,进而可解出a的范围.
解答:解:(I)由f(x)=
 +ax+b(x>-1).
+ax+b(x>-1).得到f′(x)=2x2+2x+a,
因为函数在(-1,+∞)上是单调函数,
所以f′(x)=2x2+2x+a≤0在(-1,+∞)恒成立,由于抛物线开口向上,2x2+2x+a≤0不可能成立;
所以f′(x)=2x2+2x+a≥0在(-1,+∞)恒成立,
则a≥-2x2-2x⇒a≥

所以实数a的取值范围是:[
 ,+∞).
,+∞).(II)∵函数f(x)既有极大值又有极小值
由题意f′(x)=2x2+2x+a=0在(-1,+∞)上有两解,
∴
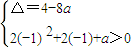 ⇒0<a<
⇒0<a<
故实数a的取值范围0<a<
 .
.点评:此题考查函数在某点取得极值的条件、考查学生会利用导函数的正负确定函数的单调区间,掌握函数恒成立时所取的条件,是一道综合题.

练习册系列答案
相关题目
设函数f(x)=a+bcosx+csinx的图象过点(0,1)和点(
,1),当x∈[0,
]时,|f(x)|<2,则实数a的取值范围是( )
| π |
| 2 |
| π |
| 2 |
A、-
| ||||
B、1≤a<4+3
| ||||
C、-
| ||||
| D、-a<a<2 |