题目内容
已知向量
=(sinωx+cosωx,sinωx)
=(sinωx-cosωx,2
cosωx),设函数f(x)=
•
(x∈R)的图象关于直线x=
对称,其中常数ω∈(0,2)
(Ⅰ)求f(x)的最小正周期;
(Ⅱ)将函数f(x)的图象向左平移
个单位,得到函数g(x)的图象,用五点法作出函数g(x)在区间[-
,
]的图象.
| a |
| b |
| 3 |
| a |
| b |
| π |
| 3 |
(Ⅰ)求f(x)的最小正周期;
(Ⅱ)将函数f(x)的图象向左平移
| π |
| 12 |
| π |
| 2 |
| π |
| 2 |
分析:(Ⅰ)由两向量的坐标,利用平面向量的数量积运算法则列出关系式,再利用两角和与差的正弦函数公式化为一个角的正弦函数,根据f(x)的图象关于直线x=
对称,得到f(
)=±2,求出k与ω的值,即可确定出f(x)的最小正周期;
(Ⅱ)利用平移规律确定出g(x)的解析式,由x的范围求出2x的范围,利用五点法即可作出g(x)的图象.
| π |
| 3 |
| π |
| 3 |
(Ⅱ)利用平移规律确定出g(x)的解析式,由x的范围求出2x的范围,利用五点法即可作出g(x)的图象.
解答:解:(Ⅰ)∵向量
=(sinωx+cosωx,sinωx)
=(sinωx-cosωx,2
cosωx),
∴f(x)=
•
=sin2ωx-cos2ωx+2
sinωxcosωx=
sin2ωx-cosωx=2sin(2ωx-
),
∵f(x)的图象关于直线x=
对称,∴f(
)=±2,
∴
ω-
=kπ+
,k∈Z,即ω=
+1∈(0,2),
∴k=0,ω=1,即f(x)=2sin(2x-
),
∴T=π;
(Ⅱ)根据题意得:g(x)=f(x+
)=2sin2x,
画出图象得:
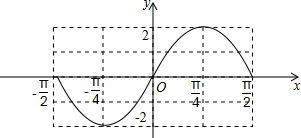
| a |
| b |
| 3 |
∴f(x)=
| a |
| b |
| 3 |
| 3 |
| π |
| 6 |
∵f(x)的图象关于直线x=
| π |
| 3 |
| π |
| 3 |
∴
| 2π |
| 3 |
| π |
| 6 |
| π |
| 2 |
| 3k |
| 2 |
∴k=0,ω=1,即f(x)=2sin(2x-
| π |
| 6 |
∴T=π;
(Ⅱ)根据题意得:g(x)=f(x+
| π |
| 12 |
| x | -
|
-
|
0 |
|
| ||||||||
| 2x | -π | -
|
0 |
|
π | ||||||||
| 2sin2x | 0 | -2 | 0 | 2 | 0 |
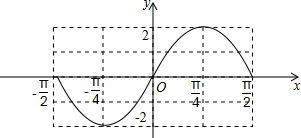
点评:此题考查了三角函数的周期性及其求法,平面向量积的运算法则,两角和与差的正弦函数公式,以及五点法画三角函数图象,熟练掌握公式是解本题的关键.

练习册系列答案
相关题目