题目内容
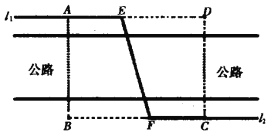
【题目】如图,某自来水公司要在公路两侧安装排水管,公路为东西方向,在路北侧沿直线![]() 排,在路南侧沿直线
排,在路南侧沿直线![]() 排,现要在矩形区域
排,现要在矩形区域![]() 内沿直线将
内沿直线将![]() 与
与![]() 接通.已知
接通.已知![]() ,
,![]() ,公路两侧排水管费用为每米1万元,穿过公路的
,公路两侧排水管费用为每米1万元,穿过公路的![]() 部分的排水管费用为每米2万元,设
部分的排水管费用为每米2万元,设![]() 与
与![]() 所成的小于
所成的小于![]() 的角为
的角为![]() .
.
(Ⅰ)求矩形区域![]() 内的排水管费用
内的排水管费用![]() 关于
关于![]() 的函数关系;
的函数关系;
(Ⅱ)求排水管的最小费用及相应的角![]() .
.
【答案】(Ⅰ)![]()
![]() ; (Ⅱ)最小费用为
; (Ⅱ)最小费用为![]() 万元,相应的角为
万元,相应的角为![]() .
.
【解析】
(Ⅰ)过![]() 作
作![]() ,垂足为
,垂足为![]() ,由题意得
,由题意得![]() ,利用三角函数的定义分别表示
,利用三角函数的定义分别表示![]() ,
,![]() 的长度,进而求解;
的长度,进而求解;
(Ⅱ)由(Ⅰ),设![]() ,要求
,要求![]() 的最小值,可先求
的最小值,可先求![]() 的最大值,利用导函数求得
的最大值,利用导函数求得![]() 的最大值,进而求解.
的最大值,进而求解.
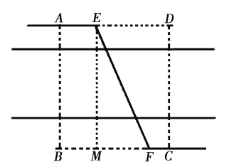
解:(Ⅰ)如图,
过![]() 作
作![]() ,垂足为
,垂足为![]() ,由题意得
,由题意得![]() ,
,
故有![]() ,
,![]() ,
,![]() ,
,
∴![]()
![]()
(Ⅱ)由(Ⅰ)设![]() ,
,
则![]()
![]() ,
,
令![]() ,得
,得![]() ,即
,即![]() ,得
,得![]() ,
,
∴当![]() 时,
时,![]() ,
,![]() 为增函数;
为增函数;
当![]() 时,
时,![]() ,
,![]() 为减函数,
为减函数,
∴当![]() 时,有
时,有![]() ,此时
,此时![]() .
.
答:排管的最小费用为![]() 万元,相应的角为
万元,相应的角为![]() .
.

【题目】“微信运动”已成为当下热门的运动方式,小王的微信朋友内也有大量好友参与了“微信运动”,他随机选取了其中的40人(男、女各20人),记录了他们某一天的走路步数,并将数据整理如下:
性别 步数 | 0~2000 | 2001~5000 | 5001~8000 | 8001~10000 | >10000 |
男 | 1 | 2 | 3 | 6 | 8 |
女 | 0 | 2 | 10 | 6 | 2 |
(1)已知某人一天的走路步数超过8000步被系统评定为“积极型”,否则为“懈怠型”,根据题意完成下面的2×2列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?
积极型 | 懈怠型 | 总计 | |
男 | |||
女 | |||
总计 |
(2)若小王以这40位好友该日走路步数的频率分布来估计其所有微信好友每日走路步数的概率分布,现从小王的所有微信好友中任选2人,其中每日走路不超过5000步的有X人,超过10000步的有Y人,设ξ=|X﹣Y|,求E的分布列及数学期望.
附:K2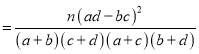 ,n=a+b+c+d.
,n=a+b+c+d.
P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 |