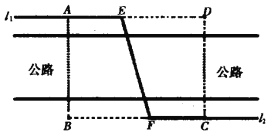
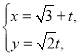题目内容
【题目】“微信运动”已成为当下热门的运动方式,小王的微信朋友内也有大量好友参与了“微信运动”,他随机选取了其中的40人(男、女各20人),记录了他们某一天的走路步数,并将数据整理如下:
性别 步数 | 0~2000 | 2001~5000 | 5001~8000 | 8001~10000 | >10000 |
男 | 1 | 2 | 3 | 6 | 8 |
女 | 0 | 2 | 10 | 6 | 2 |
(1)已知某人一天的走路步数超过8000步被系统评定为“积极型”,否则为“懈怠型”,根据题意完成下面的2×2列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?
积极型 | 懈怠型 | 总计 | |
男 | |||
女 | |||
总计 |
(2)若小王以这40位好友该日走路步数的频率分布来估计其所有微信好友每日走路步数的概率分布,现从小王的所有微信好友中任选2人,其中每日走路不超过5000步的有X人,超过10000步的有Y人,设ξ=|X﹣Y|,求E的分布列及数学期望.
附:K2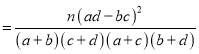 ,n=a+b+c+d.
,n=a+b+c+d.
P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 |
【答案】(1)列联表见解析,没有95%以上的把握认为“评定类型”与“性别”有关;(2)分布列见解析,E(ξ)![]()
【解析】
(1)根据题设数据完成列联表,代入公式计算即得解;
(2)ξ可能的取值为0,1,2,根据独立和互斥事件的概率公式求解对应的概率得到分布列,计算期望,即得解.
(1)根据题表中的数据完成2×2列表如下:
积极型 | 懈怠型 | 总计 | |
男 | 14 | 6 | 20 |
女 | 8 | 12 | 20 |
总计 | 22 | 18 | 40 |
K2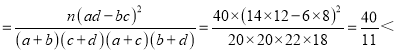 3.841,
3.841,
∴没有95%以上的把握认为“评定类型”与“性别”有关.
(2)由题意得小王的微信好友中任选一人,其每日走路频数不超过5000步的概率为![]() ,
,
超过10000步的概率为![]() ,
,
当X=Y=0或X=Y=1时,ξ=0,
P(ξ=0)![]() ,
,
当X=1,Y=0或X=0,Y=1时,ξ=1,
P(ξ=1)![]() ,
,
当X=2,Y=0或X=0,Y=2时,ξ=2,
P(ξ=2)![]() ,
,
∴ξ的分布列为:
Ξ | 0 | 1 | 2 |
P |
|
|
|
E(ξ)![]() .
.

【题目】某高校共有学生15000人,其中男生10500人,女生4500人,为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300名学生每周平均体育运动时间的样本数据(单位:小时).
(1)应收集多少位女生的样本数据?
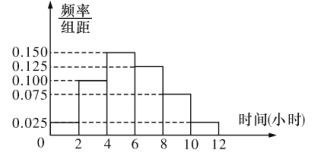
(2)根据这300个样本数据,得到学生每周平均体育运动时间的频率分布直方图(如图所示),其中样本数据的分组区间为:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,估计该校学生每周平均体育运动时间超过4小时的概率;
,估计该校学生每周平均体育运动时间超过4小时的概率;
(3)在样本数据中,有60位女生的每周平均体育运动时间超过4小时,请完成每周平均体育运动时间与性别列联表,并判断是否有![]() 的把握认为“该校学生的毎周平均体育运动时间与性别有关”.
的把握认为“该校学生的毎周平均体育运动时间与性别有关”.
男生 | 女生 | 总计 | |
每周平均体育运动时间不超过4小时 | |||
每周平均体育运动时间超过4小时 | |||
总计 |
附: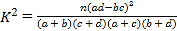 ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
【题目】2019年双十一落下帷幕,天猫交易额定格在268(单位:十亿元)人民币(下同),再创新高,比去年218(十亿元)多了50(十亿元).这些数字的背后,除了是消费者买买买的表现,更是购物车里中国新消费的奇迹,为了研究历年销售额的变化趋势,一机构统计了2010年到2019年天猫双十一的销售额数据y(单位:十亿元),绘制如表:
年份 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
编号x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
销售额y | 0.9 | 8.7 | 22.4 | 41 | 65 | 94 | 132.5 | 172.5 | 218 | 268 |
根据以上数据绘制散点图,如图所示
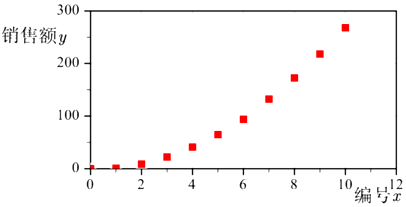
(1)根据散点图判断,![]() 与
与![]() 哪一个适宜作为销售额
哪一个适宜作为销售额![]() 关于
关于![]() 的回归方程类型?(给出判断即可,不必说明理由)
的回归方程类型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果及如表中的数据,建立![]() 关于
关于![]() 的回归方程,并预测2020年天猫双十一销售额;(注:数据保留小数点后一位)
的回归方程,并预测2020年天猫双十一销售额;(注:数据保留小数点后一位)
(3)把销售超过100(十亿元)的年份叫“畅销年”,把销售额超过200(十亿元)的年份叫“狂欢年”,从2010年到2019年这十年的“畅销年”中任取2个,求至少取到一个“狂欢年”的概率.
参考数据:![]()
|
|
|
|
|
|
参考公式:
对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计公式分别
的斜率和截距的最小二乘估计公式分别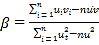 ,
,![]() .
.
【题目】某公司为了预测下月产品销售情况,找出了近7个月的产品销售量![]() (单位:万件)的统计表:
(单位:万件)的统计表:
月份代码 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
销售量 |
|
|
|
|
|
|
|
但其中数据污损不清,经查证![]() ,
,![]() ,
,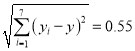 .
.
(1)请用相关系数说明销售量![]() 与月份代码
与月份代码![]() 有很强的线性相关关系;
有很强的线性相关关系;
(2)求![]() 关于
关于![]() 的回归方程(系数精确到0.01);
的回归方程(系数精确到0.01);
(3)公司经营期间的广告宣传费![]() (单位:万元)(
(单位:万元)(![]() ),每件产品的销售价为10元,预测第8个月的毛利润能否突破15万元,请说明理由.(毛利润等于销售金额减去广告宣传费)
),每件产品的销售价为10元,预测第8个月的毛利润能否突破15万元,请说明理由.(毛利润等于销售金额减去广告宣传费)
参考公式及数据:![]() ,相关系数
,相关系数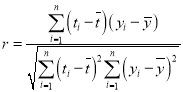 ,当
,当![]() 时认为两个变量有很强的线性相关关系,回归方程
时认为两个变量有很强的线性相关关系,回归方程![]() 中斜率和截距的最小二乘估计公式分别为
中斜率和截距的最小二乘估计公式分别为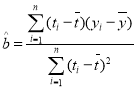 ,
,![]() .
.