题目内容
3.已知函数f(x)=$\frac{{4}^{x}}{2+{4}^{x}}$.(1)用定义证明,函数f(x)是R上的增函数;
(2)证明:对于任意实数r,都有f(t)+f(1-t)=1;
(3)求值:f($\frac{1}{2013}$)+f($\frac{2}{2013}$)+f($\frac{3}{2013}$)+…+f($\frac{2012}{2013}$)
分析 (1)直接利用用定义,通过f(x1)-f(x2)化简表达式,比较出大小即可证明函数f(x)是R上的单调性;
(2)化简f(t)+f(1-t),证明它的值是1即可;
(3)由(2),f(t)+f(1-t)=1,求出首末两项的和为1,利用倒序相加法,求出f($\frac{1}{2013}$)+f($\frac{2}{2013}$)+f($\frac{3}{2013}$)+…+f($\frac{2012}{2013}$)
解答 解:(1)证明:设任意x1<x2,
则f(x1)-f(x2)=$\frac{{4}^{{x}_{1}}}{2{+4}^{{x}_{1}}}$-$\frac{{4}^{{x}_{2}}}{2{+4}^{{x}_{2}}}$=$\frac{2{(4}^{{x}_{1}}{-4}^{{x}_{2}})}{(2{+4}^{{x}_{1}})(2{+4}^{{x}_{2}})}$,
∵x1<x2,
∴4x1<4x2,∴4x1-4x2<0,
又2+4x1>0,2+4x2>0.
∴f(x1)-f(x2)<0,
∴f(x1)<f(x2),…(4分)
∴f(x)在R上是增函数; …(6分)
(2)对任意t,f(t)+f(1-t)=$\frac{{4}^{t}}{2{+4}^{t}}$-$\frac{{4}^{t-1}}{2{+4}^{t-1}}$=$\frac{2{+4}^{t}}{2{+4}^{t}}$=1.
∴对于任意t,f(t)+f(1-t)=1; …(10分)
(3)∵由(2)得f(t)+f(1-t)=1
∴f($\frac{1}{2013}$)+f($\frac{2012}{2013}$)=1,f($\frac{2}{2013}$)+f( $\frac{2011}{2013}$)=1,
∴f($\frac{1}{2013}$)+f( $\frac{2}{2013}$)+…+f( $\frac{2012}{2013}$)+f($\frac{2012}{2013}$)+f($\frac{2011}{2013}$)+…+f($\frac{1}{2013}$)=2012,
∴f($\frac{1}{2013}$)+f($\frac{2}{2013}$)+f($\frac{3}{2013}$)+…+f($\frac{2012}{2013}$)=$\frac{2012}{2}$.…(14分)
点评 本题考查函数的单调性的证明,函数值的求法,考查计算能力,值域倒序相加法的应用.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案| A. | (2,+∞) | B. | (-∞,-1]∪(2,+∞) | C. | (-∞,-1)∪(2,+∞) | D. | [-1,0]∪[2,+∞) |
| A. | (-1,0) | B. | (-1,-$\frac{5}{11}$) | C. | [-1,-$\frac{5}{11}$) | D. | [-1,-$\frac{5}{11}$] |
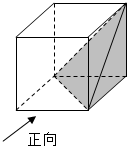 如图是正方体截去阴影部分所得的几何体,则该几何体的左视图是 ( )
如图是正方体截去阴影部分所得的几何体,则该几何体的左视图是 ( )