Question

 (本小题满分14分)

已知函数f (x)=e^x，g(x)=lnx，h(x)=kx+b.

(1)当b=0时，若对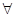x∈（0，+∞）均有f (x)≥h(x)≥g(x)成立，求实数k的取值范围；

(2)设h(x)的图象为函数f (x)和g(x)图象的公共切线，切点分别为(x₁, f (x₁))和(x₂, g(x₂))，其中x₁>0.

①求证：x₁>1>x₂；

②若当x≥x₁时，关于x的不等式ax₂－x+xe+1≤0恒成立，求实数a的取值范围.

 

Answer 1

【答案】

（1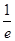）[，e]（2）①分别求f(x)和g(x)在点(x₁, f (x₁))和(x₂, g(x₂))的切线，记为公切线，所以斜率和截距分别相同，从而得证结论；②（－∞，1]

【解析】

试题分析：(1)依题意对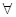x∈（0，+∞）均有e^x≥kx≥lnx成立，

即对任意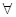x∈（0，+∞）均有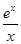≥k≥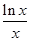成立，                         ……1分

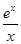∴()_min≥k≥，

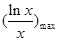因为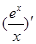=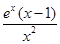，故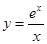在（0，1）上减，（1，+∞）增，

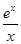∴（）_min=e，

又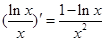 ，故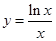在（0，e）上减，（e，+∞）增，

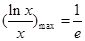∴ ，即k的取值范围是[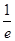，e] .                              ……5分

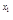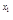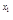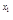(2)由题知：h(x)即为y－e= e(x－x₁)即y=e·x+ e－x₁ e,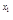

也为y=lnx₂=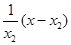即y=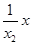+lnx₂－1,

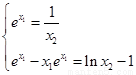∴,                                                ……6分

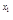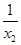又x₁=0   ∴e>1 即>1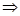x₁>1即x₁>1>x_2,                                                      ……8分

(3)令F(x)=ax₂－x+xe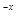+1(x≥x₁),

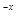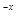∴F′(x)= －1－xe+e=－1+e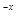(1－x)( x≥x₁₎

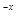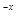又x≥x₁>1    F′(x)= －1－xe+e=－1+e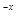(1－x)<0,

即F(x)=ax₂－x+xe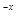+1(x≥x₁)单减,

所以只要F(x)≤F(x₁)= ax₂－x₁+₁xe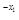+1≤0,

即a+ x₁－x₁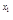e+ e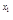≤0.                                                  ……12分

由,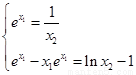

∴,

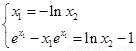即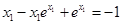

故只要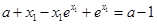≤0得：a≤1,

综上，实数a的取值范围是（－∞，1].                                    ……14分

考点：本小题主要考查利用导数研究函数的单调性、极值、最值等和利用导数求曲线的切线，和利用导数解决恒成立问题，考查学生综合运算所学知识分析问题、解决问题的能力和运算求解能力.

点评：导数是研究函数性质的有力工具，要熟练应用，而恒成立问题一般要转化为最值问题解决.