题目内容
设函数f(x)=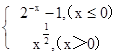 ,若f(x0)>1,则x0的取值范围是
,若f(x0)>1,则x0的取值范围是
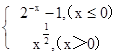 ,若f(x0)>1,则x0的取值范围是
,若f(x0)>1,则x0的取值范围是 | A.(-1,1) | B.(-1,+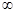 ) ) |
C.(-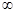 ,-1)∪(0,+ ,-1)∪(0,+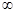 ) ) | D.(-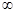 ,-1)∪(1,+ ,-1)∪(1,+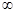 ) ) |
D
此题答案应选D
分析:将变量x0按分段函数的范围分成两种情形,在此条件下分别进行求解,最后将满足的条件进行合并.
解答:解:当x0≤0时,2-x0-1>1,则x0<-1,
当x0>0时,x0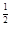 >1则x0>1,
>1则x0>1,
故x0的取值范围是(-∞,-1)∪(1,+∞),
故选D.
分析:将变量x0按分段函数的范围分成两种情形,在此条件下分别进行求解,最后将满足的条件进行合并.
解答:解:当x0≤0时,2-x0-1>1,则x0<-1,
当x0>0时,x0
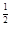 >1则x0>1,
>1则x0>1,故x0的取值范围是(-∞,-1)∪(1,+∞),
故选D.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
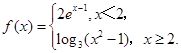 则
则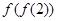 的值为 ( )
的值为 ( )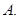
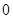
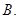
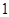
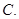
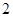
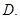
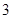
 的定义域是( )
的定义域是( )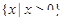
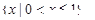
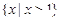
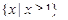
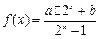 的反函数
的反函数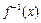 的图象过点
的图象过点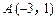 .
.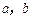 的值;
的值;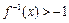
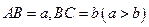 ,在AB、AD、CD、CB上分别
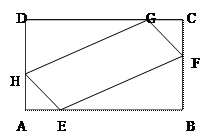
,在AB、AD、CD、CB上分别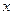 ,
,
 小题14分)已知函数
小题14分)已知函数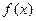 的图像与函数
的图像与函数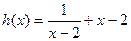 的图像关于点
的图像关于点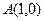 对称
对称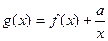 ,
,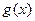 在区间
在区间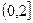 上的值不小于6,求实数a的取值范围.
上的值不小于6,求实数a的取值范围. 2+(K-1)x+3是偶函数,则f(x)的递减区间是
2+(K-1)x+3是偶函数,则f(x)的递减区间是 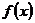 是周期函数,且满足
是周期函数,且满足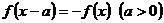 ,函数
,函数