题目内容
8．矩形ABCD中，AB=2，AD=1，E为CD的中点，沿AE将△DAE折起到△D1AE的位置，使平面D1AE⊥平面ABCE．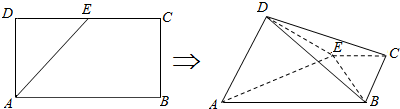
（1）求证：BE⊥D1A；
（2）求四棱锥D1-ABCE的体积．
分析 （1）在矩形ABCD中，求出AE=BE=$\sqrt{2}$，AB=2，说明AE⊥BE，然后证明BE⊥平面D1AE，即可证明结论；
（2）作D1F⊥AE于F，则D1F⊥平面ABCE，再利用体积公式求四棱锥D1-ABCE的体积．
解答 
（1）证明：∵矩形ABCD中，AB=2，AD=1，E为CD的中点．
∴AE=BE=$\sqrt{2}$，AB=2，
∴AE⊥BE，
由于平面D1AE丄平面ABCE，BE?平面ABCE，AE为平面D1AE与平面ABCE的交线，
∴BE丄平面D1AE，∴BE丄D1A…（6分）
（2）解：作D1F⊥AE于F，则D1F⊥平面ABCE，D1F=$\frac{\sqrt{2}}{2}$，…（9分）
而SABCE=$\frac{1}{2}×（1+2）×1$=$\frac{3}{2}$，
∴四棱锥D1-ABCE的体积为$\frac{1}{3}×\frac{3}{2}×\frac{\sqrt{2}}{2}$=$\frac{\sqrt{2}}{4}$．…（12分）
点评 本题考查直线与平面垂直，折叠问题，四棱锥D1-ABCE的体积的求法，考查空间想象能力，计算能力．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
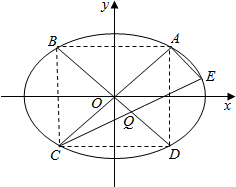设A（x0，y0）（x0，y0≠0）是椭圆T：$\frac{{x}^{2}}{m+1}$+y2=1（m＞0）上一点，它关于y轴、原点、x轴的对称点依次为B，C，D．E是椭圆T上不同于A的另外一点，且AE⊥AC，如图所示．
如图，AB是⊙O的一条切线，切点为B，ADE，CFD和 CGE都是⊙O的割线，AC=AB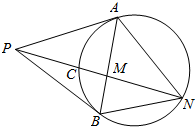
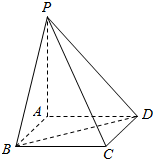已知PA垂直于矩形ABCD所在平面，PA=3，AB=1，BC=$\sqrt{3}$．