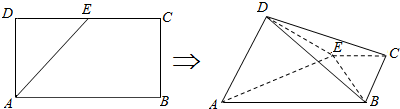
题目内容
18.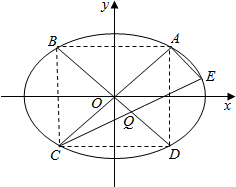 设A(x0,y0)(x0,y0≠0)是椭圆T:$\frac{{x}^{2}}{m+1}$+y2=1(m>0)上一点,它关于y轴、原点、x轴的对称点依次为B,C,D.E是椭圆T上不同于A的另外一点,且AE⊥AC,如图所示.
设A(x0,y0)(x0,y0≠0)是椭圆T:$\frac{{x}^{2}}{m+1}$+y2=1(m>0)上一点,它关于y轴、原点、x轴的对称点依次为B,C,D.E是椭圆T上不同于A的另外一点,且AE⊥AC,如图所示.(Ⅰ) 若点A横坐标为$\frac{\sqrt{3}}{2}$,且BD∥AE,求m的值;
(Ⅱ)求证:直线BD与CE的交点Q总在椭圆$\frac{{x}^{2}}{m+1}$+y2=($\frac{m}{m+2}$)2上.
分析 (Ⅰ)由对称性结合A的横坐标可得A的纵坐标,代入椭圆方程可求m的值;
(Ⅱ)设E(x1,y1),由于A,E均在椭圆T上,则$\left\{\begin{array}{l}{{{x}_{0}}^{2}+(m+1){{y}_{0}}^{2}=m+1①}\\{{{x}_{1}}^{2}+(m+1){{y}_{1}}^{2}=m+1②}\end{array}\right.$,联立可得BD所在直线方程,再由kAE•kAC=-1求出CE所在直线方程,联立两直线方程把Q的坐标用A的坐标表示,代入椭圆方程证得答案.
解答 (Ⅰ)解:∵BD∥AE,AE⊥AC,
∴BD⊥AC,可知A($\frac{\sqrt{3}}{2},\frac{\sqrt{3}}{2}$),
故$\frac{3}{m+1}=1$,m=2;
(Ⅱ)证明:由对称性可知B(-x0,y0),C(-x0,-y0),D(x0,-y0),四边形ABCD为矩形,
设E(x1,y1),由于A,E均在椭圆T上,则
$\left\{\begin{array}{l}{{{x}_{0}}^{2}+(m+1){{y}_{0}}^{2}=m+1①}\\{{{x}_{1}}^{2}+(m+1){{y}_{1}}^{2}=m+1②}\end{array}\right.$,
由②-①得:(x1+x0)(x1-x0)+(m+1)(y1+y0)(y1-y0)=0,
显然x1≠x0,从而$\frac{{y}_{1}+{y}_{0}}{{x}_{1}+{x}_{0}}=-\frac{1}{m+1}•\frac{{x}_{1}-{x}_{0}}{{y}_{1}-{y}_{0}}=-\frac{1}{m+1}$$•\frac{1}{{k}_{AE}}$=$\frac{1}{m+1}•{k}_{AC}=\frac{1}{m+1}•\frac{{y}_{0}}{{x}_{0}}$,
∵AE⊥AC,∴kAE•kAC=-1,
∴$\left\{\begin{array}{l}{y=-\frac{{y}_{0}}{{x}_{0}}x}\\{y+{y}_{0}=\frac{{y}_{1}+{y}_{0}}{{x}_{1}+{x}_{0}}(x+{x}_{0})=\frac{1}{m+1}•\frac{{y}_{0}}{{x}_{0}}(x+{x}_{0})}\end{array}\right.$,
解得$\left\{\begin{array}{l}{{x}_{0}=\frac{m+2}{m}x}\\{{y}_{0}=-\frac{m+2}{m}y}\end{array}\right.$,
代入椭圆方程,知$\frac{{x}^{2}}{m+1}+{y}^{2}=(\frac{m}{m+2})^{2}$.
点评 本题主要考查圆锥曲线的定义的应用,关键是利用椭圆的对称性寻求点的坐标间的关系,体现了整体运算思想方法,是中档题.

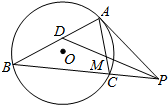 如图所示,△ABC内接于圆O,过点A的切线交BC的延长线于点P,D为AB的中点,DP交AC于点M,若BP=8,AM=4,AC=6,则PA=( )
如图所示,△ABC内接于圆O,过点A的切线交BC的延长线于点P,D为AB的中点,DP交AC于点M,若BP=8,AM=4,AC=6,则PA=( )| A. | 4$\sqrt{2}$ | B. | 3$\sqrt{2}$ | C. | $\sqrt{2}$ | D. | 5$\sqrt{2}$ |

| A. | 35° | B. | 45° | C. | 55° | D. | 70° |
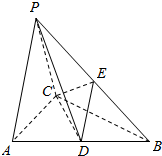 三棱锥P-ABC中△PAC是边长为4的等边三角形,△ABC为等腰直角三角形,∠ACB=90°,平面PAC⊥面 ABC,D、E分别为AB、PB的中点.
三棱锥P-ABC中△PAC是边长为4的等边三角形,△ABC为等腰直角三角形,∠ACB=90°,平面PAC⊥面 ABC,D、E分别为AB、PB的中点. 如图,△ABC中,BC=10,以 BC 为直径的圆分别交 AB,AC于点 E,F.
如图,△ABC中,BC=10,以 BC 为直径的圆分别交 AB,AC于点 E,F.