题目内容
19. 如图,AB是⊙O的一条切线,切点为B,ADE,CFD和 CGE都是⊙O的割线,AC=AB
如图,AB是⊙O的一条切线,切点为B,ADE,CFD和 CGE都是⊙O的割线,AC=AB(1)证明:AC2=AD•AE;
(2)证明:FG∥AC.
分析 (1)利用切线长与割线长的关系及AB=AC进行证明.
(2)利用成比例的线段证明角相等、三角形相似,得到同位角角相等,从而两直线平行.
解答 证明:(1)因为AB是ΘO的一条切线,AE为割线
所以AB2=AD•AE,
又因为AB=AC,所以AD•AE=AC2…(5分)
(2)由(1)得$\frac{AD}{AC}=\frac{AC}{AE}$.
∵∠EAC=∠DAC,∴△ADC∽△ACE,
∴∠ADC=∠ACE.
∵∠ADC=∠EGF,
∴∠EGF=∠ACE,
∴GF∥AC…(10分)
点评 本题考查圆的切线、割线长的关系,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的左,右焦点为F1,F2.A,B为顶点,以线段F1F2为直径的圆交双曲线的一条渐近线bx-ay=0于M,N两点,且∠MAB=30°,则双曲线的离心率为( )
| A. | $\frac{{\sqrt{21}}}{3}$ | B. | 2 | C. | $\frac{{\sqrt{6}}}{2}$ | D. | $\frac{5}{3}$ |
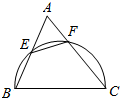 如图,△ABC中,BC=10,以 BC 为直径的圆分别交 AB,AC于点 E,F.
如图,△ABC中,BC=10,以 BC 为直径的圆分别交 AB,AC于点 E,F.