ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΡ≥ΖΰΉΑ≥ß…ζ≤ζ“Μ÷÷ΖΰΉΑΘ§ΟΩΦΰΖΰΉΑΒΡ≥…±ΨΈΣ40‘ΣΘ§≥ω≥ßΒΞΦέΈΣ60‘ΣΘ§ΗΟ≥ßΈΣΙΡάχœζ έ…ΧΕ©ΙΚΘ§ΨωΕ®Β±“Μ¥ΈΕ©ΙΚΝΩ≥§Ιΐ100Φΰ ±Θ§ΟΩΕύΕ©ΙΚ“ΜΦΰΘ§Ε©ΙΚΒΡ»Ϊ≤ΩΖΰΉΑΒΡ≥ω≥ßΒΞΦέΨΆΫΒΒΆ0.02‘ΣΘ§ΗυΨί –≥ΓΒς≤ιΘ§œζ έ…Χ“Μ¥ΈΕ©ΙΚΝΩ≤ΜΜα≥§Ιΐ500ΦΰΘ°
Θ®1Θ©…η“Μ¥ΈΕ©ΙΚΝΩΈΣxΦΰΘ§ΖΰΉΑΒΡ ΒΦ ≥ω≥ßΒΞΦέΈΣP‘ΣΘ§–¥≥ωΚ· ΐP=fΘ®xΘ©ΒΡ±μ¥ο ΫΘΜ
Θ®2Θ©Β±œζ έ…Χ“Μ¥ΈΕ©ΙΚΕύ…ΌΦΰΖΰΉΑ ±Θ§ΗΟΖΰΉΑ≥ßΜώΒΟΒΡάϊ»σΉν¥σΘΩ≤Δ«σ≥ωΉν¥σ÷ΒΘ°
ΓΨ¥πΑΗΓΩ
Θ®1Θ©ΫβΘΚ…η“Μ¥ΈΕ©ΙΚΝΩΈΣxΦΰΘ§ΖΰΉΑΒΡ ΒΦ ≥ω≥ßΒΞΦέΈΣP‘ΣΘ§
Β±0ΘΦxΓή100 ±Θ§P=60
Β±100ΘΦxΓή500 ±Θ§ ![]()
Υυ“‘ 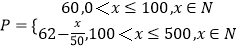
Θ®2Θ©ΫβΘΚ…ηœζ έ…Χ“Μ¥ΈΕ©ΙΚΝΩΈΣxΦΰΘ§ΙΛ≥ßΜώΒΟΒΡάϊ»σΈΣy‘ΣΘ§‘ρ”– 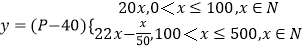
Β±0ΘΦxΓή100«“xΓ N ±Θ§“Ή÷Σx=100Θ§y»ΓΒΟΉν¥σ÷Β2000‘Σ
Β±100ΘΦxΓή500«“xΓ N ±Θ§ ![]() Θ§
Θ§
‘ρ¥ΥΚ· ΐ‘Ύ100ΘΦxΓή500«“xΓ N…œΒί‘ωΘ§Ι x=500 ±Θ§y»ΓΒΟΉν¥σ÷Β6000‘ΣΘ°
ΓΏ6000ΘΨ2000Θ§
ΓύΒ±œζ έ…Χ“Μ¥ΈΕ©ΙΚ500ΦΰΖΰΉΑ ±Θ§ΗΟΖΰΉΑ≥ßΜώΒΟΒΡΉν¥σάϊ»σ6000‘Σ
ΓΨΫβΈωΓΩΘ®1Θ©άϊ”ΟΖ÷ΕΈΚ· ΐ÷±Ϋ”Ν–≥ωΚ· ΐΒΡΫβΈω ΫΦ¥Ω…Θ°Θ®2Θ©άϊ”ΟΘ®1Θ©Ν–≥ωάϊ»σΚ· ΐΘ§Ζ÷±π«σΫβΖ÷ΕΈΚ· ΐΒΡΉν÷ΒΘ§ΆΤ≥ωΫαΙϊΦ¥Ω…Θ°