题目内容
【题目】已知数列{an}的前n项和为Sn ， 且Sn=2an﹣2（n∈N*）．
（1）求数列{an}的通项公式；
（2）若数列{bn}满足 
= 
﹣ 
﹣…+（﹣1）n+1 
，求数列{bn}的通项公式；
（3）在（2）的条件下，设cn=2n+λbn ， 问是否存在实数λ使得数列{cn}（n∈N*）是单调递增数列？若存在，求出λ的取值范围；若不存在，请说明你的理由．
【答案】
（1）解：由Sn=2an﹣2（n∈N*），可得a1=2a1﹣2，解得a1=2；
n≥2时，an=Sn﹣Sn﹣1=2an﹣2﹣（2an﹣1﹣2），化为：an=2an﹣1．
∴数列{an}是等比数列，公比为2，首项为2．∴an=2n．
（2）解：∵ 
= 
= 
﹣ 
﹣…+（﹣1）n+1 
，
∴ 
= ﹣ ﹣…+ 
，
∴ 
=（﹣1）n+1 ，∴bn=（﹣1）n 
．
当n=1时， 
= 
，解得b1= 
．∴bn=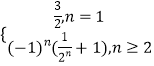 
．
（3）解：cn=2n+λbn，
∴n≥3时，cn=2n+λ 
，cn﹣1=2n﹣1+（﹣1）n﹣1λ 
，
cn﹣cn﹣1=2n﹣1+ 
＞0，即（﹣1）nλ＞﹣ 
．
① 当n为大于或等于4的偶数时，λ＞﹣ ，即λ＞﹣ 
，当且仅当n=4时，λ＞﹣ 
．
②当n为大于或等于3的奇数时，λ＜ ，当且仅当n=3时，λ＜ 
．
当n=2时，c2﹣c1= 
﹣ 
＞0，即λ＜8．
综上可得：λ的取值范围是 
．
【解析】（1）由Sn=2an﹣2（n∈N*），可得a1=2a1﹣2，解得a1=2；n≥2时，an=Sn﹣Sn﹣1 ， 化为：an=2an﹣1 ． 即可得出．（2） = = ﹣ ﹣…+（﹣1）n+1 ，n≥2时， = ﹣ ﹣…+ ，相减可得：bn=（﹣1）n ．当n=1时， = ，解得b1= ．（3）cn=2n+λbn ， n≥3时，cn=2n+λ ，cn﹣cn﹣1=2n﹣1+ ＞0，即（﹣1）nλ＞﹣ ．①当n为大于或等于4的偶数时，λ＞﹣ ．②当n为大于或等于3的奇数时，λ＜ 
．当n=2时，c2﹣c1＞0，即λ＜8．即可得出．
【考点精析】认真审题，首先需要了解数列的前n项和(数列{an}的前n项和sn与通项an的关系
)，还要掌握数列的通项公式(如果数列an的第n项与n之间的关系可以用一个公式表示，那么这个公式就叫这个数列的通项公式)的相关知识才是答题的关键．
