题目内容
圆心在直线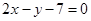 上的圆C与
上的圆C与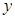 轴交于两点
轴交于两点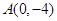 ,
,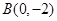 ,则圆C的方程为 .
,则圆C的方程为 .
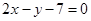 上的圆C与
上的圆C与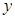 轴交于两点
轴交于两点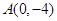 ,
,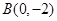 ,则圆C的方程为 .
,则圆C的方程为 .(x-2)2+(y+3)2=5
由垂径定理确定圆心所在的直线,再由条件求出圆心的坐标,根据圆的定义求出半径即可.
解:∵圆C与y轴交于A(0,-4),B(0,-2),
∴由垂径定理得圆心在y=-3这条直线上.
又∵已知圆心在直线2x-y-7=0上,∴联立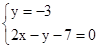 ,解得x=2,
,解得x=2,
∴圆心为(2,-3),
∴半径r=|AC|=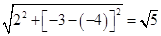 .
.
∴所求圆C的方程为(x-2)2+(y+3)2=5.
故答案为(x-2)2+(y+3)2=5.
解:∵圆C与y轴交于A(0,-4),B(0,-2),
∴由垂径定理得圆心在y=-3这条直线上.
又∵已知圆心在直线2x-y-7=0上,∴联立
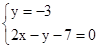 ,解得x=2,
,解得x=2,∴圆心为(2,-3),
∴半径r=|AC|=
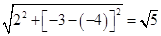 .
.∴所求圆C的方程为(x-2)2+(y+3)2=5.
故答案为(x-2)2+(y+3)2=5.

练习册系列答案
相关题目
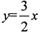 上,且其横坐标为整数,又圆C截直线
上,且其横坐标为整数,又圆C截直线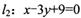 所得的弦长为
所得的弦长为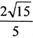 •
•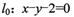 上,过点P作圆的两条切线PA, PB,切点分别为A ,B求四边形PACB面积的最小值.
上,过点P作圆的两条切线PA, PB,切点分别为A ,B求四边形PACB面积的最小值.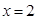 被圆
被圆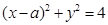 所截得的弦长等于
所截得的弦长等于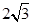 ,则
,则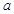 的值为
的值为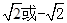
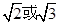
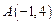 的圆的圆心为
的圆的圆心为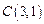 .
.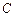 的方程;
的方程;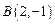 的直线
的直线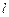 被圆
被圆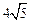 ,求直线
,求直线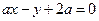 与圆
与圆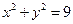 的位置关系是( )
的位置关系是( )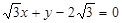 截圆x2+y2=4得的劣弧所对的圆心角是( )
截圆x2+y2=4得的劣弧所对的圆心角是( ) 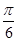
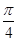
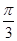
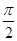
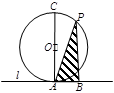
 的内部,则
的内部,则 的取值范围是( )
的取值范围是( )



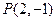 为圆
为圆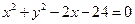 的弦
的弦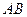 的中点,则弦
的中点,则弦