题目内容
8.化简:sin($\frac{π}{4}$-3x)cos($\frac{π}{3}$-3x)-cos($\frac{π}{6}$+3x)sin($\frac{π}{4}$+3x)
分析 由条件利用诱导公式、两角和的正弦公式化简所给的式子,可得结果.
解答 解:sin($\frac{π}{4}$-3x)cos($\frac{π}{3}$-3x)-cos($\frac{π}{6}$+3x)sin($\frac{π}{4}$+3x)
=sin($\frac{π}{4}$-3x)cos($\frac{π}{3}$-3x)-sin($\frac{π}{3}$-3x)cos($\frac{π}{4}$-3x)
=sin[($\frac{π}{4}$-3x)-($\frac{π}{3}$-3x)]=sin(-$\frac{π}{12}$)
=-sin$\frac{π}{12}$.
点评 本题主要考查诱导公式、两角和的正弦公式的应用,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.已知a=${log}_{2}\frac{1}{3}$,b=lg5,c=ln$\sqrt{e}$,则a、b、c的大小关系为( )
| A. | <b<a | B. | c<a<b | C. | a<c<b | D. | a<b<c |
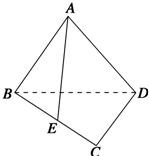 如图,在等腰直角三角形ABD中,∠BAD=90°,且等腰直角三角形ABD与等边三角形CBD所在平面垂直,E为BC的中点,则AE与平面BCD所成角的大小为45°.
如图,在等腰直角三角形ABD中,∠BAD=90°,且等腰直角三角形ABD与等边三角形CBD所在平面垂直,E为BC的中点,则AE与平面BCD所成角的大小为45°.