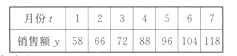
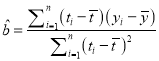题目内容
【题目】已知函数![]() ,其中
,其中![]() .
.
(I)若a=1,求![]() 在区间[0,3]上的最大值和最小值;
在区间[0,3]上的最大值和最小值;
(II)解关于x的不等式![]() .
.
【答案】(Ⅰ)最小值为![]() ,最大值为
,最大值为![]() ;(Ⅱ)答案见解析.
;(Ⅱ)答案见解析.
【解析】试题分析:(1)当![]() 时,
时, ![]() ,根据二次函数的性质能求出
,根据二次函数的性质能求出![]() 在
在![]() 上的最大值和最小值;(2)当
上的最大值和最小值;(2)当![]() 时,原不等式等价于
时,原不等式等价于![]() ,当
,当![]() 时,原不等式等价于
时,原不等式等价于![]() ,由此根据一元二次不等式的解法能求出当
,由此根据一元二次不等式的解法能求出当![]() 时,不等式的解集为
时,不等式的解集为![]() 或
或![]() ,当
,当![]() 时,不等式的的解集为
时,不等式的的解集为![]() ;当
;当![]() 时,不等式的解集为
时,不等式的解集为![]() ;当
;当![]() 时,不等式的解集为
时,不等式的解集为![]() .
.
试题解析:(![]() )当
)当![]() 时,
时, ![]() ,
,
∴函数![]() 在
在![]() 上是减函数,在
上是减函数,在![]() 上是增函数,
上是增函数,
∴![]() 在
在![]() 上的最小值为
上的最小值为![]() ,
,
又![]() ,
, ![]() ,
, ![]() ,
,
∴![]() 在
在![]() 上的最大值为
上的最大值为![]() .
.
(![]() )(i)当
)(i)当![]() 时,原不等式等价于
时,原不等式等价于![]() ,
,
∵![]() ,
,
∴![]() ,
,
此时![]() 的解集为
的解集为![]() 或
或![]() .
.
(ii)当![]() 时,原不等式等价于
时,原不等式等价于![]() ,
,
由![]() ,得:
,得:
①若![]() ,则
,则![]() ,此时
,此时![]() 的解集为
的解集为![]() ;
;
②当![]() ,原不等式无解;
,原不等式无解;
③当![]() ,则
,则![]() ,此时,
,此时, ![]() 的解集为
的解集为![]() ,
,
综上,当![]() 时,不等式的解集为
时,不等式的解集为![]() 或
或![]() ,
,
当![]() 时,不等式的解集为
时,不等式的解集为![]() ,
,
当![]() 时,不等式的解集为
时,不等式的解集为![]() ,
,
当![]() 时,不等式的解集为
时,不等式的解集为![]() .
.

练习册系列答案
相关题目