题目内容

7．从正方形四个顶点中任取2个点，则这2个点间的距离大于该正方形边长的概率为（　　）
A．$\frac{1}{6}$B．$\frac{1}{3}$C．$\frac{1}{2}$D．$\frac{2}{3}$

分析 利用列举法分别列举出对应事件的个数，结合古典概型的概率公式进行求解即可．

解答 解：从正方形ABCD四个顶点中任取2个点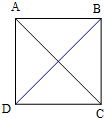，有AB，BC，CD，DA，AC，BD共有6种结果，
若这2个点间的距离大于该正方形边长，则为AC，BD，2个结果，
则对应的概率P=$\frac{2}{6}=\frac{1}{3}$，
故选：B

点评 本题主要考查概率的计算，利用列举法是解决本题的关键．

练习册系列答案
相关题目
9．给出下列四个命题：
①y=2+x3sin（x+$\frac{5π}{2}$）在区间[-10π，10π]上的最大值与最小值之和是6；
②函数f（x）=$\frac{x-1}{2x+1}$（x≠-$\frac{1}{2}$）的对称中心是（-$\frac{1}{2}$，-$\frac{1}{2}$）；
③底面是等边三角形，侧面都是等腰三角形的三棱锥是正三棱锥；
④已知函数y=2sin（ωx+φ）（ω＞0，0＜φ＜π）为偶函数，其图象与直线y=2的交点的横坐标为x1，x2，若|x1-x2|的最小值为π，则ω=2，φ=$\frac{π}{2}$
所有正确命题的序号是④．
18．若函数f（x）=2sinxcosx+2$\sqrt{3}$cos2x-$\sqrt{3}$
（Ⅰ）求函数f（x）的单调递增区间；
（Ⅱ）当$x∈[{0，\frac{π}{2}}]$时，求函数f（x）的值域．
15．如图，己知E、F、G、H分别是三棱锥A-BCD的棱AB、BC、CD、DA的中点．
①求证：E、F、G、H四点共面
②若四边形EFGH是矩形，求证，AC⊥BD．
2．已知函数f（x）=ax2+bx-$\frac{3}{4}$（a＞0），g（x）=4x+$\frac{2^x}{b}$+$\frac{1}{4}$，且y=f（x+$\frac{1}{4a}}$）为偶函数．设集合A={x|t-1≤x≤t+1}．
（Ⅰ）若t=-$\frac{b}{2a}$，记f（x）在A上的最大值与最小值分别为M，N，求M-N；
（Ⅱ）若对任意的实数t，总存在x1，x2∈A，使得|f（x1）-f（x2）|≥g（x）对?x∈[0，1]恒成立，试求a的最小值．
12．如图，在△OAB中，P为线段AB上的一点，若$\overrightarrow{{O}{P}}$=x$\overrightarrow{{O}{A}}$+y$\overrightarrow{{O}{B}}$，且$\overrightarrow{{B}{P}}$=2$\overrightarrow{{P}{A}}$，则$\frac{x}{y}$等于（　　）
A．$\frac{1}{2}$B．$\frac{1}{3}$C．1D．2
19．在三棱锥A-BCD中，底面BCD是正三角形，AC=BD=2，AB=AD=$\sqrt{2}$，O为BC的中点．
（1）求证：AO⊥平面BCD；
（2）求二面角A-DC-B的余弦值．
16．某几何体的正视图，侧视图及俯视图均如图所示，则该几何体的体积为（　　）
A．$\frac{4}{3}$B．$\frac{8}{3}$C．$\sqrt{6}$D．2$\sqrt{6}$
17．从两块玉米地里各抽取10株玉米苗，分别测得它们的株高如下（单位：cm ）：
甲：25 41 40 37 22 14 19 39 21 42        
乙：27 16 44 27 44 16 40 40 16 40
根据以上数据回答下面的问题：并用数据说明下列问题．
（1）哪种玉米苗长得高？
（2）哪种玉米苗长得齐？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网