题目内容
【题目】已知四棱锥![]() 中,底面
中,底面![]() 为直角梯形,
为直角梯形, ![]() 平面
平面![]() ,侧面
,侧面![]() 是等腰直角三角形,
是等腰直角三角形, ![]() ,
, ![]() ,点
,点![]() 是棱
是棱![]() 的中点.
的中点.
(1)证明:平面![]() 平面
平面![]() ;
;
(2)求锐二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析(2) ![]()
【解析】,
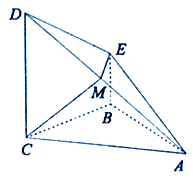
试题分析:(1)取AC的中点F,连接BF,可证![]() 平面ACD,又可证四边形BFME是平行四边形.可得 EM//BF,可证
平面ACD,又可证四边形BFME是平行四边形.可得 EM//BF,可证![]() 平面ACD,从而平面
平面ACD,从而平面![]() 平面
平面![]() ;(2)利用空间直角坐标进行向量运算,根据法向量夹角即可求出.
;(2)利用空间直角坐标进行向量运算,根据法向量夹角即可求出.
试题解析:
(1)证明:取AC的中点F,连接BF,
因为AB=BC,所以![]() ,
, ![]() 平面ABC,所以CD
平面ABC,所以CD ![]() .
.
又![]() 所以
所以![]() 平面ACD.①
平面ACD.①
因为AM=MD,AF=CF,所以![]() .
.
因为![]()
![]() ,所以
,所以![]() //MF,
//MF,
所以四边形BFME是平行四边形.所以EM//BF.②
由①②,得![]() 平面ACD,所以平面
平面ACD,所以平面![]() 平面
平面![]() ;
;
(2)解: ![]() BE
BE![]() 平面ABC,
平面ABC,
![]() 又
又![]() ,
,
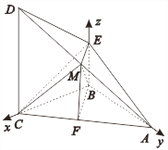
![]() 以点B为原点,直线BC、BA、BE分别为x,y,z轴,
以点B为原点,直线BC、BA、BE分别为x,y,z轴,
建立空间直角坐标系B-xyz.
由![]() ,得B(0,0,0),C(2,0,0),A(0,2,0),D(2,0,2).
,得B(0,0,0),C(2,0,0),A(0,2,0),D(2,0,2).
由中点坐标公式得![]() ,
, ![]() ,
,![]() ,
,
设向量![]() 为平面BMC的一个法向量,则
为平面BMC的一个法向量,则![]() 即
即![]()
令y=1,得x=0,z=-1,即![]() ,
,
由(I)知, ![]() 是平面ACD的一个法向量.
是平面ACD的一个法向量.
设二面角B-CM-A的平面角为![]() ,
,
则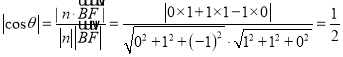 ,
,
又二面角B-CM-A为锐二面角,故![]() .
.

 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案【题目】已知椭圆![]() 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在![]() 轴上,离心率
轴上,离心率![]() ,且椭圆
,且椭圆![]() 经过点
经过点![]() ,过椭圆
,过椭圆![]() 的左焦点
的左焦点![]() 且不与坐标轴垂直的直线交椭圆
且不与坐标轴垂直的直线交椭圆![]() 于
于![]() ,
, ![]() 两点.
两点.
(1)求椭圆![]() 的方程;
的方程;
(2)设线段![]() 的垂直平分线与
的垂直平分线与![]() 轴交于点
轴交于点![]() ,求△
,求△![]() 的面积
的面积![]() 的取值范围.
的取值范围.
【题目】某大学为调研学生在A,B两家餐厅用餐的满意度,从在A,B两家餐厅都用过餐的学生中随机抽取了100人,每人分别对这两家餐厅进行评分,满分均为60分.
整理评分数据,将分数以![]() 为组距分成
为组距分成![]() 组:
组: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
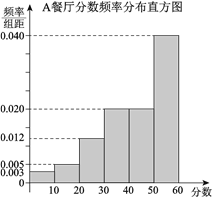
, ![]() ,得到A餐厅分数的频率分布直方图,和B餐厅分数的频数分布表:
,得到A餐厅分数的频率分布直方图,和B餐厅分数的频数分布表:
B餐厅分数频数分布表 | |
分数区间 | 频数 |
|
|
|
|
|
|
|
|
|
|
|
|
定义学生对餐厅评价的“满意度指数”如下:
分数 |
|
|
|
满意度指数 |
|
|
|
(Ⅰ)在抽样的100人中,求对A餐厅评价“满意度指数”为![]() 的人数;
的人数;
(Ⅱ)从该校在A,B两家餐厅都用过餐的学生中随机抽取1人进行调查,试估计其对A餐厅评价的“满意度指数”比对B餐厅评价的“满意度指数”高的概率;
(Ⅲ)如果从A,B两家餐厅中选择一家用餐,你会选择哪一家?说明理由.
