题目内容
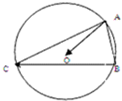△ABC的外心为O，角A，B，C的对边分别为a，b，c，若b=| 3 |
| AO |
| BC |
分析：取BC中点D，连接OD，AD，则DO⊥BC，利用向量的运算，可得
•
=
(
2-
2)，由此可得结论．
| AO |
| BC |
| 1 |
| 2 |
| AC |
| AB |
解答：解：取BC中点D，连接OD，AD，则DO⊥BC
∴
•
=(
+
)•
=
•
=
(
+
)•(
-
)=
(
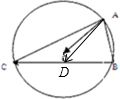
2-
2)
∵b=
，c=1，
∴
(
2-
2)=
×(3-1)=1
∴
•
=1
故选B．
∴
| AO |
| BC |
| AD |
| DO |
| BC |
| AD |
| BC |
| 1 |
| 2 |
| AB |
| AC |
| AC |
| AB |
| 1 |
| 2 |
| AC |
| AB |
∵b=
| 3 |
∴
| 1 |
| 2 |
| AC |
| AB |
| 1 |
| 2 |
∴
| AO |
| BC |
故选B．
点评：本题考查向量的运算，考查学生的计算能力，解题的关键是熟练掌握向量的三角形法则，属于中档题．
练习册系列答案
名校课堂系列答案
相关题目
设△ABC的外心为O，以线段OA、OB为邻边作平行四边形，第四个顶点为D，再以OC、OD为邻边作平行四边形，它的第四个顶点为H．
设△ABC的外心为O，重心为G，取点H，使
设△ABC的外心为O（三角形外接圆的圆心），其外接圆半径为1，以线段OA、OB为邻边作平行四边形，第四个顶点为D，再以OC，OD为邻边作平行四边形，它的第四个顶点为H．若