题目内容
已知△ABC的外心为O，
•
=8，则|
|=（ ）
| AO |
| AB |
| AB |
分析：过O点作OD垂直AB于D，可由垂径定理得D为AB的中点．根据向量数量积的定义，
•
=|
||
| cos∠OAB=
|
| 2=8，故可得|
|=4
| AO |
| AB |
| AO |
| AB |
| 1 |
| 2 |
| AB |
| AB |
解答：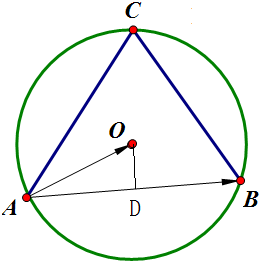
解：如图，过O点作OD⊥AB于D，则由垂径定理得 AD=
AB
Rt△AOD中，cos∠OAB=
=
所以
•
=|
||
| cos∠OAB
=|
||
| ×
=
|
|2
又∵
•
=8
∴
|
|2=8，得|
|=4
故选B
解：如图，过O点作OD⊥AB于D，则由垂径定理得 AD=| 1 |
| 2 |
Rt△AOD中，cos∠OAB=
| AD |
| AO |
| 1 |
| 2 |
| AB |
| AO |
所以
| AO |
| AB |
| AO |
| AB |
=|
| AO |
| AB |
| 1 |
| 2 |
|
| ||
|
|
| 1 |
| 2 |
| AB |
又∵
| AO |
| AB |
∴
| 1 |
| 2 |
| AB |
| AB |
故选B
点评：本题主要考查向量在几何中的应用，以及向量数量积的几何意义，属中档题．解题中应该注意会巧妙的转化问题，利用直角三角形三角函数的事定义，问题化繁为简．
练习册系列答案
黄冈经典趣味课堂系列答案
启东小题作业本系列答案
相关题目
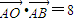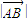，则
=（ ）
，则
=（ ）