题目内容
19.若函数f(x)=$\left\{\begin{array}{l}{x+{2}^{x},x≤0}\\{ax-lnx,x>0}\end{array}\right.$,在其定义域上恰有两个零点,则正实数a的值为$\frac{1}{e}$.分析 当x≤0时,f(x)=x+2x,单调递增,由f(-1)f(0)<0,可得f(x)在(-1,0)有且只有一个零点;x>0时,f(x)=ax-lnx有且只有一个零点,即有a=$\frac{lnx}{x}$有且只有一个实根.令g(x)=$\frac{lnx}{x}$,求出导数,求得单调区间,极值,即可得到a的值.
解答 解:当x≤0时,f(x)=x+2x,单调递增,
f(-1)=-1+2-1<0,f(0)=1>0,
由零点存在定理,可得f(x)在(-1,0)有且只有一个零点;
则由题意可得x>0时,f(x)=ax-lnx有且只有一个零点,
即有a=$\frac{lnx}{x}$有且只有一个实根.
令g(x)=$\frac{lnx}{x}$,g′(x)=$\frac{1-lnx}{{x}^{2}}$,
当x>e时,g′(x)<0,g(x)递减;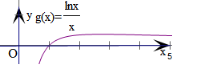
当0<x<e时,g′(x)>0,g(x)递增.
即有x=e处取得极大值,也为最大值,且为$\frac{1}{e}$,
如图g(x)的图象,当直线y=a(a>0)与g(x)的图象
只有一个交点时,则a=$\frac{1}{e}$.
故答案为:$\frac{1}{e}$.
点评 本题考查函数的零点的判断,考查函数的零点存在定理和导数的运用:求单调区间和极值,属于中档题.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
14.某校对某班50名学生进行了作业量多少的调查,得到如下列联表(单位:名):喜欢玩电脑游戏与认为作业多少列联表
能否在犯错误的概率不超过0.025的前提下认为喜欢玩电脑游戏与认为作业多之间有关系吗?为什么?
附参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
| 认为作业多 | 认为作业不多 | 总计 | |
| 喜欢玩电脑游戏 | 18 | 9 | 27 |
| 不喜欢玩电脑游戏 | 8 | 15 | 23 |
| 总计 | 26 | 24 | 50 |
附参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
4.已知随机变量ξ服从正态分布,其概率分布密度函数$f(x)=\frac{1}{{\sqrt{2π}}}{e^{-\frac{{{{({x-1})}^2}}}{2}}}$,则下列结论中错误的是( )
| A. | Eξ=1 | B. | p(0<ξ<2)=1-2p(ξ≥2) | ||
| C. | 若η=ξ-1,则η~N(0,1) | D. | Dξ=2 |
