题目内容
 (1)如图,AB是⊙O的直径,AC是弦,∠BAC的平分线AD交⊙O于D,DE⊥AC交AC延长线于点E,OE交AD于点F.
(1)如图,AB是⊙O的直径,AC是弦,∠BAC的平分线AD交⊙O于D,DE⊥AC交AC延长线于点E,OE交AD于点F.(Ⅰ)求证:DE是⊙O的切线;
(Ⅱ)若
| AC |
| AB |
| 3 |
| 5 |
| AF |
| DF |
(2)在直角坐标系中,以原点为极点,x轴的正半轴为极轴建坐标系,已知曲线
C:ρsin2θ=2acosθ(a>0),已知过点P(-2,-4)的直线L的参数方程为:
|
(Ⅰ)写出曲线C和直线L的普通方程;
(Ⅱ)若|PM|,|MN|,|PN|成等比数列,求a的值.
分析:(1)(Ⅰ)连接OD,可得∠OAD=∠OAD=∠DAC,可得OD∥AE,再由AE⊥DE,OD⊥DE,证得DE是⊙O的切线.
(Ⅱ)过D作DH⊥AB于H,求出cos∠DOH=cos∠CAN=
=
.再由△ADE∽△ADB以及△AEF∽△ODF,可得
=
=
.
(2)(Ⅰ)把曲线C方程的两边同时乘以ρ 可得 ρ2sin2θ=2a•ρ•cosθ,再根据极坐标与直角坐标的互化公式求出它的直角坐标方程,由直线L的参数方程消去参数t,求出它的普通方程.
(Ⅱ)把直线l的参数方程代入 y2=2ax,再利用根与系数的关系,求出t1+t2 和t1•t2 的值,代入|MN|2=|PM||PN|,求出a的值.
(Ⅱ)过D作DH⊥AB于H,求出cos∠DOH=cos∠CAN=
| AC |
| AB |
| 3 |
| 5 |
| AF |
| DF |
| AE |
| DO |
| 5 |
| 8 |
(2)(Ⅰ)把曲线C方程的两边同时乘以ρ 可得 ρ2sin2θ=2a•ρ•cosθ,再根据极坐标与直角坐标的互化公式求出它的直角坐标方程,由直线L的参数方程消去参数t,求出它的普通方程.
(Ⅱ)把直线l的参数方程代入 y2=2ax,再利用根与系数的关系,求出t1+t2 和t1•t2 的值,代入|MN|2=|PM||PN|,求出a的值.
解答:解:(1)(Ⅰ)证明:连接OD,可得∠OAD=∠OAD=∠DAC,∴OD∥AE.
又 AE⊥DE,OD⊥DE,∴DE是⊙O的切线.-----(6分)
(Ⅱ)过D作DH⊥AB于H,则有∠DOH=∠CAN,∴cos∠DOH=cos∠CAN=
=
.------(6分)
设 OD=5x,则 AB=10x,OH=3x,DH=4x.
∴AH=8x,AD2=80x2,-----(8分)
由△ADE∽△ADB可得 AD2=AE•AB=AE•10x,∴AE=8x.
又△AEF∽△ODF,
=
=
.------(12分)
(2)解:(Ⅰ)已知曲线C:ρsin2θ=2acosθ(a>0),即ρ2sin2θ=2a•ρ•cosθ,即 y2=2ax.
直线L的参数方程
,两式相减可得 y=x-2.-------(6分)
(Ⅱ)直线l的参数方程为
(t为参数),
代入 y2=2ax得到 t2-2
(4+a)t +8(4+a)=0,
则有 t1+t2=2
(4+a),t1•t2=8(4+a),-----------(8分)
因为|MN|2=|PM||PN|,所以(t1-t2)2=(t1+t2)2-4 t1•t2=t1•t2,
解得 a=1.-----------(12分)
又 AE⊥DE,OD⊥DE,∴DE是⊙O的切线.-----(6分)
(Ⅱ)过D作DH⊥AB于H,则有∠DOH=∠CAN,∴cos∠DOH=cos∠CAN=
| AC |
| AB |
| 3 |
| 5 |
设 OD=5x,则 AB=10x,OH=3x,DH=4x.
∴AH=8x,AD2=80x2,-----(8分)
由△ADE∽△ADB可得 AD2=AE•AB=AE•10x,∴AE=8x.
又△AEF∽△ODF,
| AF |
| DF |
| AE |
| DO |
| 5 |
| 8 |
(2)解:(Ⅰ)已知曲线C:ρsin2θ=2acosθ(a>0),即ρ2sin2θ=2a•ρ•cosθ,即 y2=2ax.
直线L的参数方程
|
(Ⅱ)直线l的参数方程为
|
代入 y2=2ax得到 t2-2
| 2 |
则有 t1+t2=2
| 2 |
因为|MN|2=|PM||PN|,所以(t1-t2)2=(t1+t2)2-4 t1•t2=t1•t2,
解得 a=1.-----------(12分)
点评:本题主要考查把参数方程化为普通方程的方法,等比数列的定义和性质,圆的切线判定定理的应用,属于基础题.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
 选作题,本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.
选作题,本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤. (2013•盐城二模)(选修4-1:几何证明选讲)
(2013•盐城二模)(选修4-1:几何证明选讲)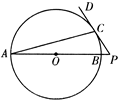 (1)如图,AB是圆O的直径,P在AB的延长线上,PD切圆O于点C.已知圆O半径为y=x-1(1≤x≤2),OP=2,则PC=
(1)如图,AB是圆O的直径,P在AB的延长线上,PD切圆O于点C.已知圆O半径为y=x-1(1≤x≤2),OP=2,则PC= ,求
,求 的值.
的值. ,直线L与曲线C分别交于M,N.
,直线L与曲线C分别交于M,N.