��Ŀ����
��1����ͼ��AB�ǡ�O��ֱ����AC���ң���BAC��ƽ����AD����O��D��DE��AC��AC�ӳ����ڵ�E��OE��AD�ڵ�F��������֤��DE�ǡ�O�����ߣ�
������
 ����
���� ��ֵ��
��ֵ����2����ֱ������ϵ�У���ԭ��Ϊ���㣬x���������Ϊ���Ὠ����ϵ����֪����
C����sin2��=2acos�ȣ�a��0������֪����P��-2��-4����ֱ��L�IJ�������Ϊ��
 ��ֱ��L������C�ֱ���M��N��
��ֱ��L������C�ֱ���M��N������д������C��ֱ��L����ͨ���̣�
������|PM|��|MN|��|PN|�ɵȱ����У���a��ֵ��

���𰸡���������1����������OD���ɵá�OAD=��OAD=��DAC���ɵ�OD��AE������AE��DE��OD��DE��֤��DE�ǡ�O�����ߣ�
����D��DH��AB��H�����cos��DOH=cos��CAN= =
= �����ɡ�ADE�ס�ADB�Լ���AEF�ס�ODF���ɵ�
�����ɡ�ADE�ס�ADB�Լ���AEF�ס�ODF���ɵ� =
= ��
��
��2����������C���̵�����ͬʱ���Ԧ� �ɵ� ��2sin2��=2a•��•cos�ȣ��ٸ��ݼ�������ֱ������Ļ�����ʽ�������ֱ�����귽�̣���ֱ��L�IJ���������ȥ����t�����������ͨ���̣�
����ֱ��l�IJ������̴��� y2=2ax�������ø���ϵ���Ĺ�ϵ�����t1+t2 ��t1•t2 ��ֵ������|MN|2=|PM||PN|�����a��ֵ��
����⣺��1������֤��������OD���ɵá�OAD=��OAD=��DAC����OD��AE��
�� AE��DE��OD��DE����DE�ǡ�O�����ߣ�-----��6�֣�
����D��DH��AB��H������DOH=��CAN����cos��DOH=cos��CAN= =
= ��------��6�֣�
��------��6�֣�
�� OD=5x���� AB=10x��OH=3x��DH=4x��
��AH=8x��AD2=80x2��-----��8�֣�
�ɡ�ADE�ס�ADB�ɵ� AD2=AE•AB=AE•10x����AE=8x��
�֡�AEF�ס�ODF�� =
= ��------��12�֣�
��------��12�֣�
��2���⣺������֪����C����sin2��=2acos�ȣ�a��0��������2sin2��=2a•��•cos�ȣ��� y2=2ax��
ֱ��L�IJ������� ����ʽ����ɵ� y=x-2��-------��6�֣�
����ʽ����ɵ� y=x-2��-------��6�֣�
����ֱ��l�IJ�������Ϊ ��tΪ��������
��t��������
���� y2=2ax�õ� ��
��
���� t1+t2=2 ��4+a����t1•t2=8��4+a����-----------��8�֣�
��4+a����t1•t2=8��4+a����-----------��8�֣�
��Ϊ|MN|2=|PM||PN|������ =
= -4 t1•t2=t1•t2��
-4 t1•t2=t1•t2��
��� a=1��-----------��12�֣�
������������Ҫ����Ѳ������̻�Ϊ��ͨ���̵ķ������ȱ����еĶ�������ʣ�Բ�������ж�������Ӧ�ã����ڻ����⣮
����D��DH��AB��H�����cos��DOH=cos��CAN=
 =
= �����ɡ�ADE�ס�ADB�Լ���AEF�ס�ODF���ɵ�
�����ɡ�ADE�ס�ADB�Լ���AEF�ס�ODF���ɵ� =
= ��
����2����������C���̵�����ͬʱ���Ԧ� �ɵ� ��2sin2��=2a•��•cos�ȣ��ٸ��ݼ�������ֱ������Ļ�����ʽ�������ֱ�����귽�̣���ֱ��L�IJ���������ȥ����t�����������ͨ���̣�
����ֱ��l�IJ������̴��� y2=2ax�������ø���ϵ���Ĺ�ϵ�����t1+t2 ��t1•t2 ��ֵ������|MN|2=|PM||PN|�����a��ֵ��
����⣺��1������֤��������OD���ɵá�OAD=��OAD=��DAC����OD��AE��
�� AE��DE��OD��DE����DE�ǡ�O�����ߣ�-----��6�֣�
����D��DH��AB��H������DOH=��CAN����cos��DOH=cos��CAN=
 =
= ��------��6�֣�
��------��6�֣��� OD=5x���� AB=10x��OH=3x��DH=4x��
��AH=8x��AD2=80x2��-----��8�֣�
�ɡ�ADE�ס�ADB�ɵ� AD2=AE•AB=AE•10x����AE=8x��
�֡�AEF�ס�ODF��
 =
= ��------��12�֣�
��------��12�֣���2���⣺������֪����C����sin2��=2acos�ȣ�a��0��������2sin2��=2a•��•cos�ȣ��� y2=2ax��
ֱ��L�IJ�������
 ����ʽ����ɵ� y=x-2��-------��6�֣�
����ʽ����ɵ� y=x-2��-------��6�֣�����ֱ��l�IJ�������Ϊ
 ��t��������
��tΪ������������ y2=2ax�õ�
 ��
������ t1+t2=2
 ��4+a����t1•t2=8��4+a����-----------��8�֣�
��4+a����t1•t2=8��4+a����-----------��8�֣���Ϊ|MN|2=|PM||PN|������
 =
= -4 t1•t2=t1•t2��
-4 t1•t2=t1•t2����� a=1��-----------��12�֣�
������������Ҫ����Ѳ������̻�Ϊ��ͨ���̵ķ������ȱ����еĶ�������ʣ�Բ�������ж�������Ӧ�ã����ڻ����⣮

��ϰ��ϵ�д�
 ��������������������ϵ�д�
��������������������ϵ�д�
�����Ŀ
 ѡ���⣬�������A��B��C��D��С�⣬��ѡ���������⣬������Ӧ�Ĵ����������������������������ǰ�������֣����ʱӦд������˵����֤�����̻����㲽�裮
ѡ���⣬�������A��B��C��D��С�⣬��ѡ���������⣬������Ӧ�Ĵ����������������������������ǰ�������֣����ʱӦд������˵����֤�����̻����㲽�裮 ��2013•�γǶ�ģ����ѡ��4-1������֤��ѡ����
��2013•�γǶ�ģ����ѡ��4-1������֤��ѡ���� ��1����ͼ��AB�ǡ�O��ֱ����AC���ң���BAC��ƽ����AD����O��D��DE��AC��AC�ӳ����ڵ�E��OE��AD�ڵ�F��
��1����ͼ��AB�ǡ�O��ֱ����AC���ң���BAC��ƽ����AD����O��D��DE��AC��AC�ӳ����ڵ�E��OE��AD�ڵ�F��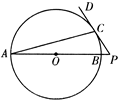 ��1����ͼ��AB��ԲO��ֱ����P��AB���ӳ����ϣ�PD��ԲO�ڵ�C����֪ԲO�뾶Ϊy=x-1��1��x��2����OP=2����PC=
��1����ͼ��AB��ԲO��ֱ����P��AB���ӳ����ϣ�PD��ԲO�ڵ�C����֪ԲO�뾶Ϊy=x-1��1��x��2����OP=2����PC=